Devil's lines

Calculus Level 4

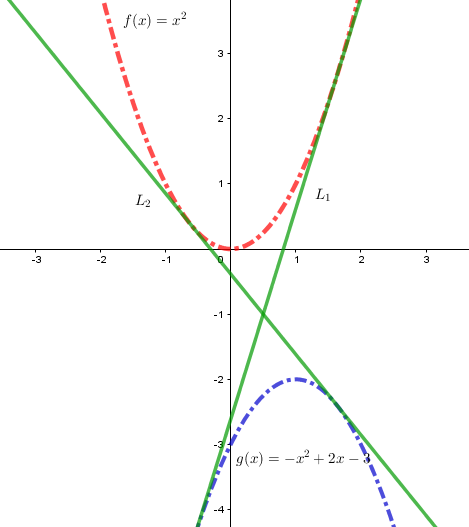
The lines $L_1$ y $L_2$ are simultaneously tangent to the graphs of $f(x)=x^2$ and $g(x)=-x^2+2x-3$ , see the figure below. The smallest angle between this two lines in the intersetion point $(a,b)$ can be represented as $\theta=\tan^{-1} \left(\frac{n\varphi-m}{p}\right),$ for $n,m$ and $p$ positive integers where $gcd(n,m)=2$ , $gcd(n,p)=1$ , $gcd(m,p)=1$ .

Find $2a+b+n+m+p$ .

$Notation:$ $\varphi=\frac{1+\sqrt{5}}{2}$ .

The answer is 9.

1 solution

Romeo Gomez
Nov 20, 2018

Suppose that the line $L_1$ is tangent to the point $(a,a^2)$ , so $L_1$ can be described by the equation $L_1(x)=2ax-a^2,$ but the same line can be described by another equation with the function $g$ , using the point $(-b,-b^2-2b-3)$ we get $L_1(x)=(2b+2)x+b^2-3,$ now, we need to solve the system

$2a=2b+2$ $-a^2=b^2-3$

solving, we obtain

$a_1=\varphi,\qquad b_1=\varphi -1$ $a_2=-\frac{1}{\varphi}, \qquad b_2=-\varphi$

hence the lines equations are

$L_1(x)=2\varphi x-\varphi^2$ $L_2(x)=(-2\varphi+2)x+\varphi^2-3$

where $\varphi=\frac{1+\sqrt{5}}{2}$ .

The intersection of these lines is the point $(\frac{1}{2},-1)$ . Using the formula for angle between lines we obtain $\theta=\tan^{-1}\left(\frac{4\varphi-2}{3}\right),$ so $2a=1,b=-1,n=4,m=2$ and $p=3$ , hence $2a+b+n+m+p=9$

Devil's lines

The answer is 9.

1 solution

0 pending reports