Diagonal Circles in a square
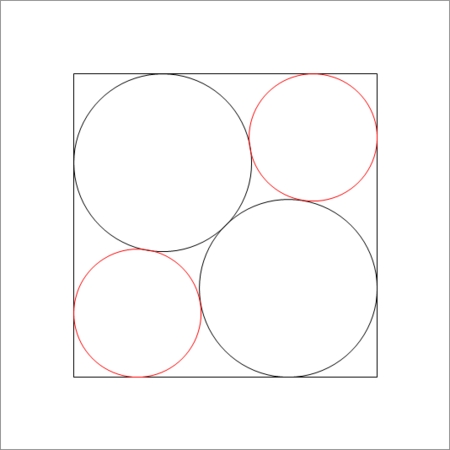
Two congruent black circles are placed diagonally in a unit square such that they touch each other at the center of the square. We want to place two red circles along the other diagonal such that they touch the sides of the square and the two black circles as shown in the figure above. Find the radius of each of the red circles. If the radius is , then enter as your answer.
The answer is 2105.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Let the radius of the large congruent circle be r . Considering the diagonal for top-left vertex to bottom-right vertex of the square, we note that:
2 r + 2 2 r = 2 ⟹ r = 2 + 2 1 = 1 − 2 1
Now consider the other diagonal:
2 2 R + 2 ( r + R ) 2 − r 2 2 R + 2 ( 2 r R + R 2 ) 4 r R + 2 R 2 4 r R + 2 R 2 2 R 2 − 4 ( 1 + r ) R + 1 2 R 2 − ( 8 − 2 2 ) R + 1 ⟹ R ⌊ 1 0 4 R ⌋ = 2 = 1 = 1 − 2 R = 4 R 2 − 4 R + 1 = 0 = 0 = 2 − 2 1 ± 4 − 2 2 ≈ 0 . 2 1 0 5 0 = 2 1 0 5 Squaring both sides Note that r = 1 − 2 1 Since R < 1