Diagonal Mystery
Points A , B , C , D are lying on a square of integer side length such that each point divides the corresponding side into integer segments.
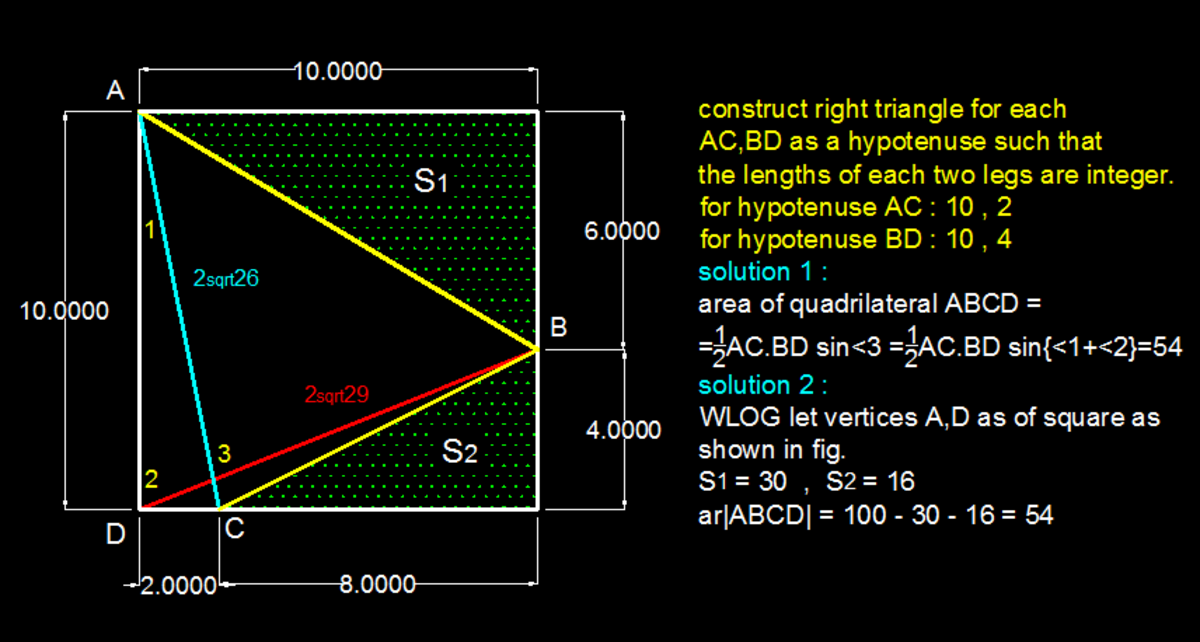
If A C = 2 2 6 and B D = 2 2 9 , what is the maximum area of quadrilateral A B C D ?
The answer is 54.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
L e t h o r i z o n t a l d i s t a n c e b e t w e e n A a n d C b e X . L e t v e r t i c a l d i s t a n c e b e t w e e n B a n d D b e Y . S t h e s i d e s o f t h e s q u a r e . ∴ S 2 + X 2 = A C 2 = ( 2 2 6 ) 2 = 1 0 4 . ∴ S 2 + Y 2 = B D 2 = ( 2 2 9 ) 2 = 1 1 6 S i n c e S , X , Y a r e i n t e g e r s , a n d A C > S , a n d B D > S , S < 1 1 . I f S = 1 0 , w e g e t X = A C 2 − S 2 = 2 , a n d Y = B D 2 − S 2 = 4 . T h i s s a t i s f i e s g i v e n d a t a . L e t P Q R S b e t h e s q u a r e . L e t A = P , B = Q . S o C R = 1 0 − 2 = 8 , a n d S D = 1 0 − 4 = 6 . S o a r e a o u t o f A B C D b u t i n P Q R S i s a s u n d e r . P S D = 2 1 ∗ 1 0 ∗ 6 = 3 0 . C R D = 2 1 ∗ 4 ∗ 8 = 1 6 . 3 0 + 1 6 = 4 6 . ∴ A r e a A B C D = 1 0 2 − 4 6 = 5 4 .
By drawing the perpendicular lines from points A , B , C , D to meet one another as shown above, we can see that each blue triangle has the same area with each red neighboring triangle. The beige rectangle is, thus, the excess area to be computed.
Let the square side length = s , the rectangle's width = x , and length = y . Then by Pythagorean theorem, A C 2 = 1 0 4 = x 2 + s 2 and B D 2 = 1 1 6 = y 2 + s 2 .
Hence, y 2 − x 2 = 1 1 6 − 1 0 4 = 1 2 = ( y − x ) ( y + x ) .
Since all the points divide the side lengths into integers, x & y are also integers.
1 2 = 1 × 1 2 = 2 × 6 = 3 × 4 .
Since ( y + x ) + ( y − x ) = 2 y , which is even, the only combination that leads to even sum is y − x = 2 and y + x = 6 .
Therefore, x = 2 and y = 4 . Then s = 1 0 .
As a result the blue area = 2 1 0 2 − 2 × 4 = 4 6 .
Finally, the area of A B C D = 4 6 + 8 = 5 4 .
The areas can be illustrated as shown below: