Diagonal Sum

Algebra Level 3

Integers from 1 to 10000 are written orderly in a grid of 100 × 100 100\times 100 , as shown in the table below.

What is the sum of the numbers in the two diagonals highlighted in yellow?


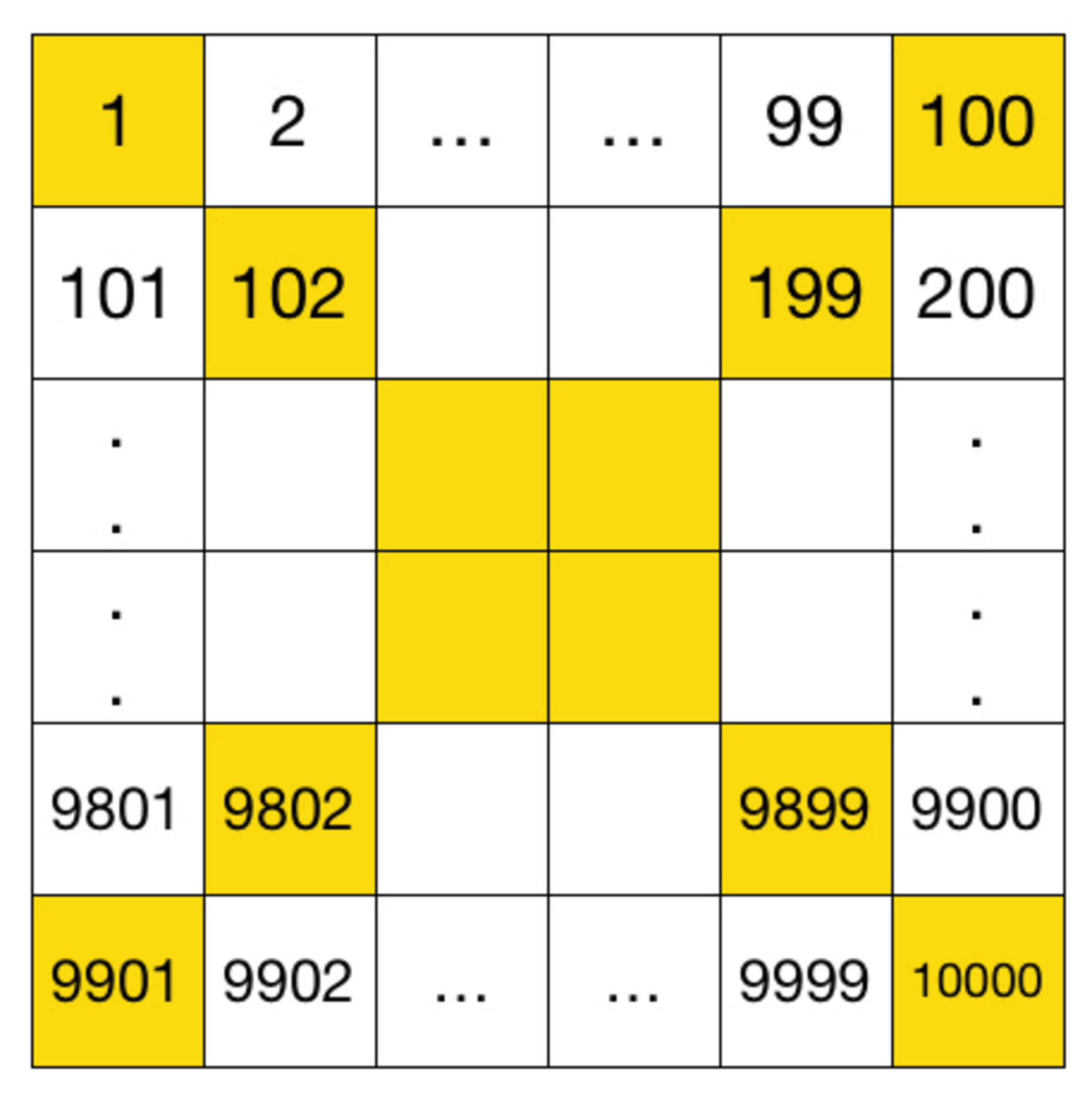
The answer is 1000100.

View wiki
Paola Ramírez by Paola Ramírez , 24, Mexico

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

2 solutions

Hugsy Bojangles
Jun 27, 2016

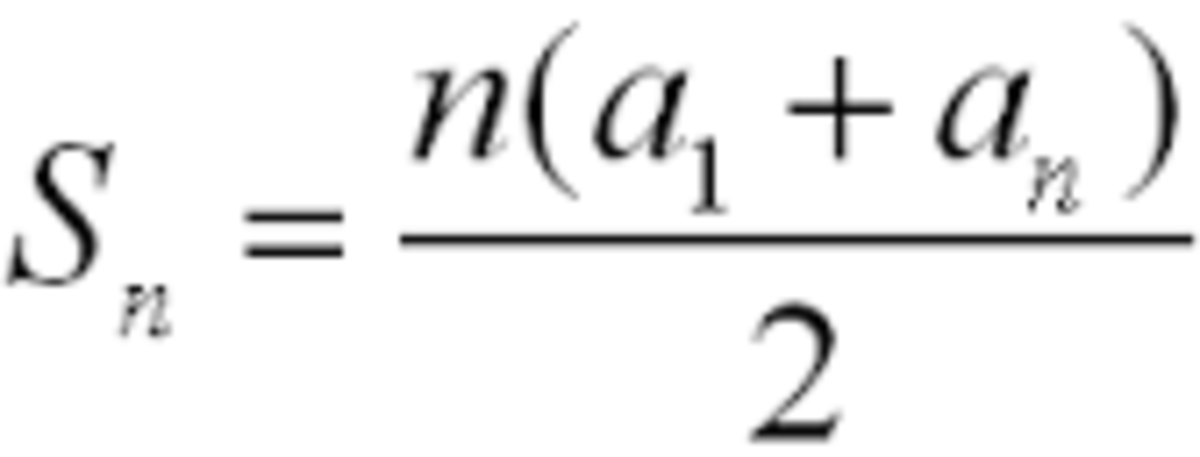
Top left and bottom right cells add to 10001, as do the bottom left and top right. This pattern continues for all highlighted cells towards the middle. Since the square is 100x100, there will be 50 pairs of numbers adding to 10001 on each diagonal and since there are two diagonals there are 100 pairs. Thus 100 x 10001 = 1000100.

5 Helpful 0 Interesting 0 Brilliant 0 Confused

The first row contributes 1 and 100. Resulting in 101. The second contributes 102 and 199. Resulting in 301. Looks like a pattern is forming. The penultimate row yields 9802+9899 = 19701. And the final row yields 9901+10000 = 19901. So, clearly, we have a hundred-element arithmetic progression. First element is 101. Last element is 19901. Number of elements 100. So, the sum, according to the formula

is

100/2 * (101 + 19901) = 1000100.

1 Helpful 0 Interesting 0 Brilliant 0 Confused

Moderator note:

Can you explain why we have an arithmetic progression?

Interesting observation. But, I am not counting the cells, instead I am only looking at the sum of the left and right boxes. Also, given that there are 100 rows, there's no "middle" row. The crossover happens between the 50th and 51st rows.

Rajendran Dandapani - 4 years, 11 months ago

Log in to reply

Oops​, I got confused by the image, which showed a "single cell". Sorry, editing my comment.

Calvin Lin Staff - 4 years, 11 months ago

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...