Diagonal Triangle of a Cuboid
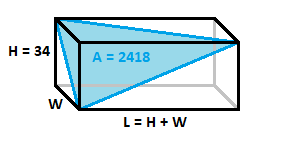
Find the volume of a cuboid whose shortest side has a length of 34, whose longest side is the sum of the other two side lengths, and whose inner triangle formed by its three different diagonals has an area of 2418.
The answer is 125120.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
I took somewhat of a brute force approach, solving the equation ∣ ∣ ( L , 0 , H ) × ( 0 , W , H ) ∣ ∣ = ∣ ∣ ( 3 4 + W , 0 , 3 4 ) × ( 0 , W , 3 4 ) ∣ ∣ = 2 × 2 4 1 8 . After a bit of computation we find W ( W + 3 4 ) + 3 4 2 = 4 8 3 6 so W ( W + 3 4 ) = 3 6 8 0 and the volume of the cuboid is 3 4 W ( W + 3 4 ) = 1 2 5 1 2 0 .
The dimensions of this cuboid is 3 4 × W × ( 3 4 + W ) , where W ≥ 3 4 .
By Pythagorean theorem , the side lengths of the triangle in question are 3 4 2 + W 2 , 3 4 2 + ( 3 4 + W ) 2 , W 2 + ( 3 4 + W ) 2 . Let a , b , c denote the these side lengths, respectively. Then, using one of the formula of Heron's formula , we have 2 4 1 8 = 4 1 ( a 2 + b 2 + c 2 ) 2 − 2 ( a 4 + b 4 + c 4 ) . With ⎩ ⎪ ⎨ ⎪ ⎧ a 2 = 3 4 2 + W 2 b 2 = 3 4 2 + ( 3 4 + W ) 2 c 2 = W 2 + ( 3 4 + W ) 2 , the equation simplifies to ( 2 4 1 8 ⋅ 4 ) 2 = 4 ( W 2 + 3 4 W + 1 1 5 6 ) 2 ⟹ W = 4 6 . The volume of the cuboid is simply 3 4 W ( 3 4 + W ) = 1 2 5 1 2 0 .