Ladder

Geometry Level 2

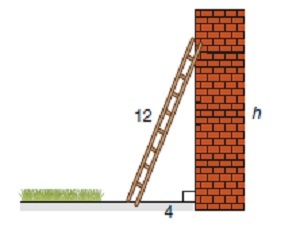
A 12 feet long ladder is leaning against a wall so that its base is 4 feet from the wall at ground level (see figure above). How far up the wall does the ladder reach?

Note: Give your answer in feet.

129 \sqrt{129} None of these choices 8 2 8\sqrt{2} 160 \sqrt{160}

View wiki
A Former Brilliant Member by A Former Brilliant Member

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

2 solutions

by the Pythagorean Theorem, we have

h 2 + 4 2 = 1 2 2 h^2 + 4^2 = 12^2

h 2 + 16 = 144 h^2 + 16 = 144

h 2 = 144 − 16 h^2 = 144 - 16

h 2 = 128 h^2 = 128

h = 128 = s q r t ( 64 ) ( 2 ) = 8 2 h = \sqrt{128} = sqrt{(64)(2)} = 8\sqrt{2} feet

1 Helpful 0 Interesting 0 Brilliant 0 Confused

Relevant wiki: Pythagorean Theorem

Using the pythagorean theorem , we have

h = 1 2 2 − 4 2 = 128 = 64 ⋅ 2 = 8 2 ⋅ 2 = 8 2 h=\sqrt{12^2-4^2}=\sqrt{128}=\sqrt{64 \cdot 2}=\sqrt{8^2 \cdot 2 }=\boxed{8\sqrt{2}}

0 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...