Diagonals of a cube
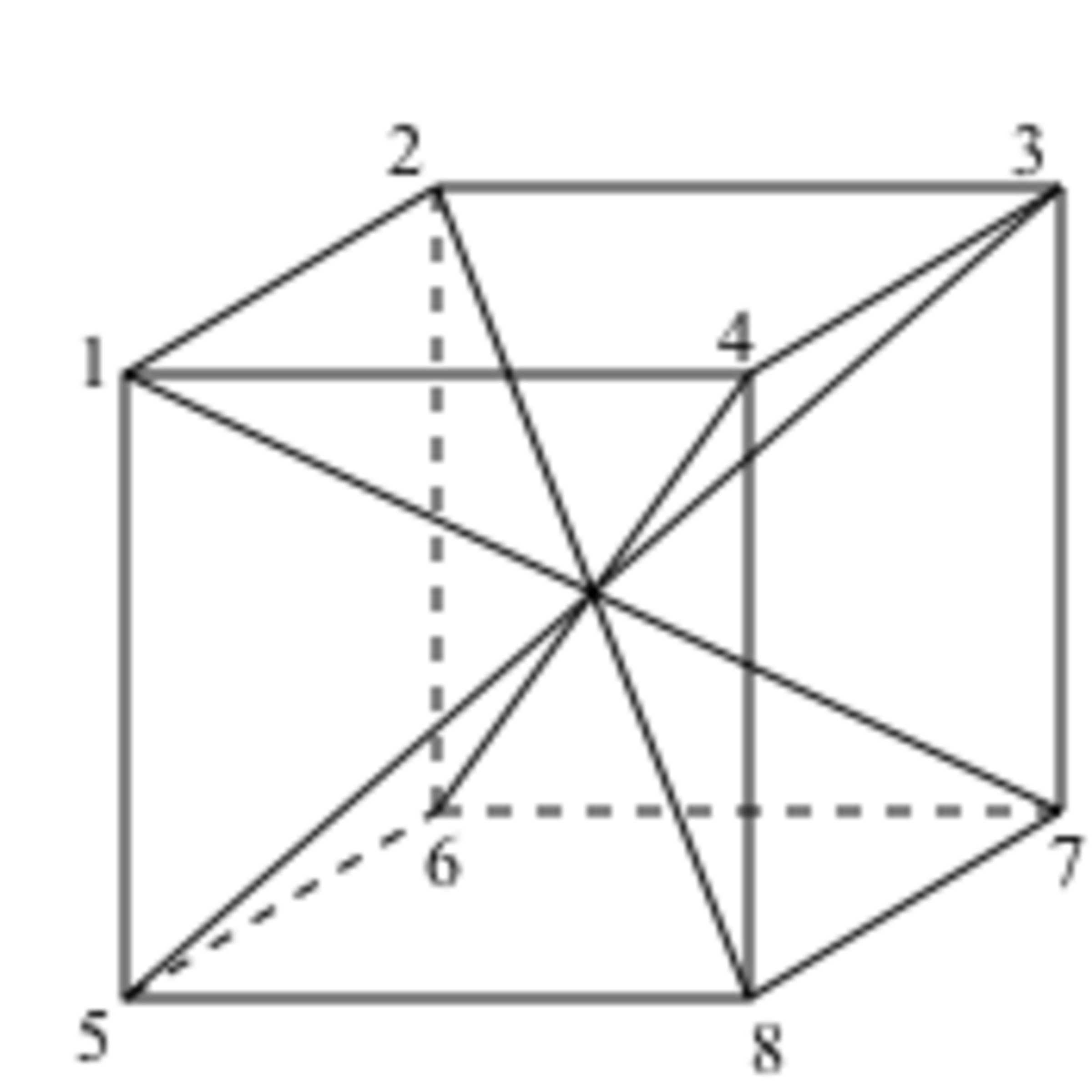
A line makes angles α , β , γ , δ with the four diagonals of a cube.
If cos 2 α + cos 2 β + cos 2 γ + cos 2 δ can be written as b a , where a and b are coprime positive integers, find a + b .
The answer is 7.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Consider the given line to be one of the four diagonals.
If side of the cube is
a
, lengths of half diagonals is
2
a
3
By using cosine rule --
We get
c
o
s
α
=
c
o
s
β
=
c
o
s
γ
=
3
1
&
c
o
s
δ
=
1
so,
b
a
=
3
4
hence,
a
+
b
=
7
A cube is rectangular parallelepiped having equal length, breadth and height. Let OADBFEGC be the cube with each side of length a units. The four diagonals are OE, AF, BG and CD.
The direction cosines of the diagonal OE which is the like joining two points O and E are
√ 3 1 , √ 3 1 , √ 3 1
Similarly, the direction cosines of AF, BG and CD are √ 3 − 1 , √ 3 1 , √ 3 1 ; √ 3 1 , √ 3 − 1 , √ 3 1 ; √ 3 1 , √ 3 1 , √ 3 − 1 respectively.
Let l , m , n be the direction cosines of the given line which makes makes angles α, β, γ, 𝛿 with OE, AF, BG, CD respectively.
Then, cos α = √ 3 1 ( l + m + n ); cos β = √ 3 1 ( − l + m + n )
cos γ = √ 3 1 ( l − m + n ); cos 𝛿 = √ 3 1 ( l + m − n )
Squaring and adding, we get
c o s 2 α + c o s 2 β + c o s 2 γ + \(cos^2 𝛿\) = 3 1 [ ( l + m + n ) 2 + ( − l + m + n ) 2 + ( l − m + n ) 2 + ( l + m − n ) 2 ]
= 3 1 [ 4 ( l 2 + m 2 + n 2 )
As l 2 + m 2 + n 2 = 1
3 1 [ 4 ( l 2 + m 2 + n 2 ) = 3 4
Where a = 4, b = 3
a + b = 4 + 3 = 7 .
Therefore the Answer is 7 .