Dicey Expectation

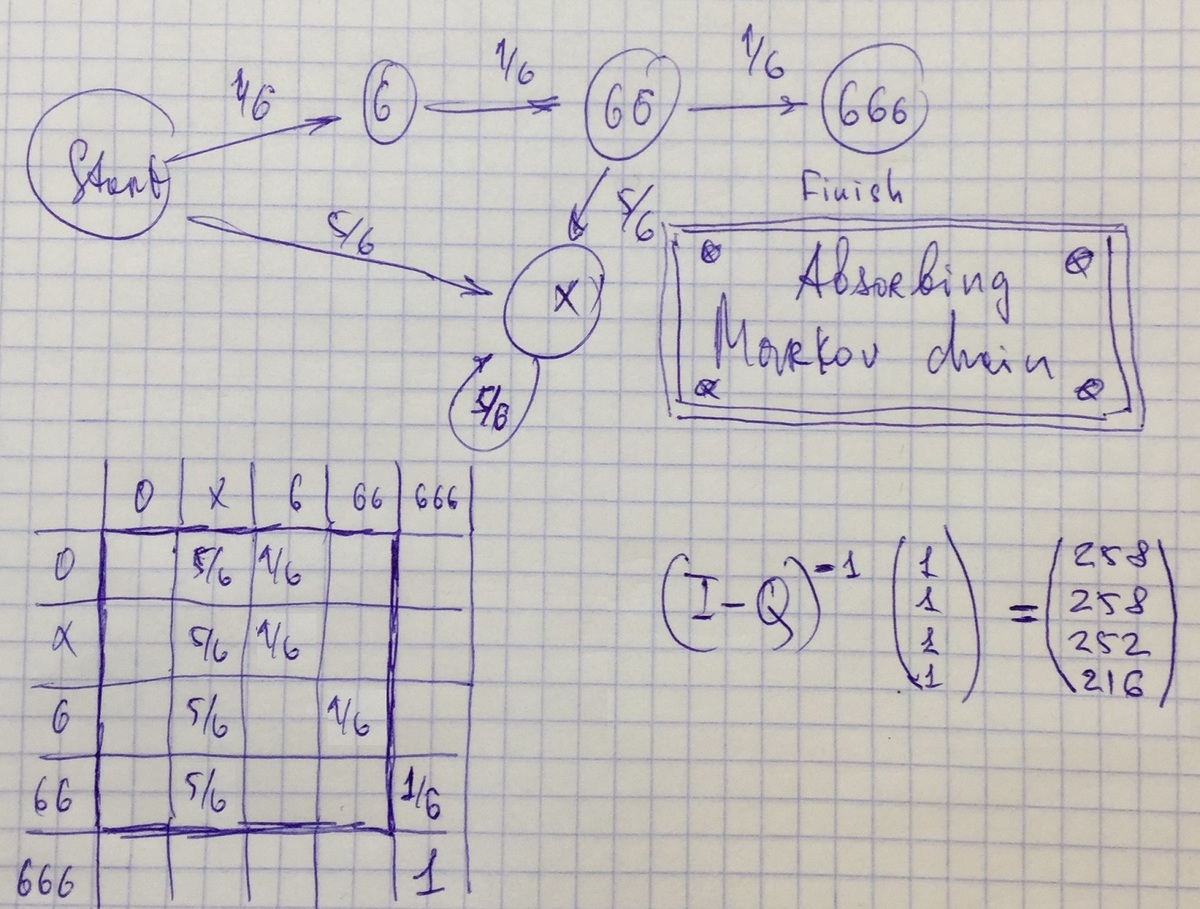
Let $E$ be the Expected number of throws. Note that if we ever get a number other than $6$ , then since the throws are independent, we would have to start over again.

If the first throw results in a number other than $6$ , the probability is $\frac {5}{6}$ and the game restarts.

If the first and second throws result in a $6$ , then a number other than $6$ , the probability is $\frac {5}{36}$ and the game restarts.

If the first, second and third throws result in a $6, 6$ , then a number other than $6$ , the probability is $\frac {5}{216}$ and the game restarts.

If the first, second, and third throws result in a $6, 6, 6$ , the probability is $\frac {1}{216}$ and the game is over.

Hence, by the linearity of expectation, we get

$E= \frac {5}{6} \times (E+1) + \frac {5}{36}\times (E+2) + \frac {5}{216} \times (E+3) + \frac {1}{216} \times 3$ .

Solving the equation, we get $E=258$ .

Absorbing Markov chain

WolframAlpha