Dicey Probability
Satvik and Agnishom are playing a game with
standard dice. Both the dice are rolled together and the total is counted.
Satvik says that a total of will be rolled first.
Agnishom, whereas, says that two Consecutive totals of will be rolled first.
They keep rolling the dice till one of them wins!
The probability that Satvik wins the game can be expressed as where and are co-prime positive integers.
Find the value of .
The answer is 20.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
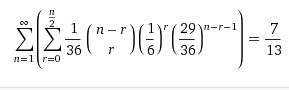
Let the probability that Satvik wins the game be P.
There are 5 possibilities.
1) If the first roll is a 2 (probability 1/36), Satvik wins immediately.
2) If the first roll is a 7, and the 2nd roll is a 2, (1/6 *1/36 = 1/216) Satvik wins immediately
3) If the first two rolls are both 7, (1/6 *1/6= 1/36) Satvik loses.
4) If the first roll is a 7 and the 2nd roll is neither a 7 nor a 2, (1/6 * 29/36 = 29/216), Satvik is back to square one and can win with probability P.
5) if the first roll is neither a 7 nor a 2, (29/36), Satvik is again back to square one and can win with probability P.
Probability P is the weighted mean of all the above possibilities,
P = 1/36 + 1/216 + (29/216) P + (29/ 36) P
Solving P = 7/13
Answer is 7 + 13 = 20