Dicier Probability...
 Satvik and Agnishom are playing a game with two standard six- sided dice. The pair of dice is rolled, and the total is recorded down.
Satvik and Agnishom are playing a game with two standard six- sided dice. The pair of dice is rolled, and the total is recorded down.
Satvik says that two seven's (not necessarily consecutive) will be rolled first.
Agnishom, says that both a six and an eight (not necessarily consecutive) will be rolled first.
The dice are repeatedly rolled till one of them wins!
What is the percentage probability that Agnishom wins the game, i.e. in other words, what is the percentage chance of throwing both a six and an eight before throwing two sevens?
The answer is 54.558.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
This problem can be easily pictured by structuring it as a Markov Chain, as per the illustration.
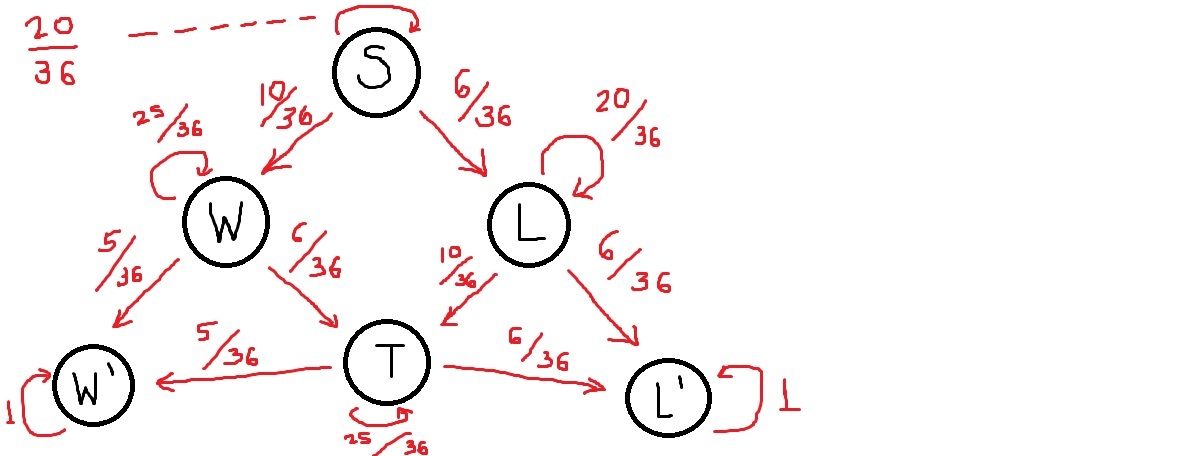
S represents the start, W a win for Agnishom, L a loss, T a current tie and W' and L' a definitive win/loss, respectively. Note that at first the chances of winning start at 10/36, which later decreases to 5/36 when one of his numbers is struck down.
We want to calculate the absorption probability of S with regards to W'. Thus, a(W') is 1 and a(L') is 0. We can derive then the remaining absorption probabilities:
a(T) is equal to 3 6 5 × a ( W ′ ) + 3 6 2 5 × a ( T ) + 3 6 6 × a ( L ′ ) Plugging the corresponding values for a(W') and a(L'), we get that a(T) = 5/11.
a(W) is equal to 3 6 5 × a ( W ′ ) + 3 6 2 5 × a ( W ) + 3 6 6 × a ( T ) Plugging the corresponding values for a(W') and a(T), we get that a(W) = 85/121.
a(L) is equal to 3 6 1 0 × a ( T ) + 3 6 2 0 × a ( L ) + 3 6 6 × a ( L ′ ) Plugging the corresponding values for a(L') and a(T), we get that a(L) = 25/88.
To top it off, we get the information from a(W) and a(L) to discover our desired a(S), which must correspond to 3 6 1 0 × a ( W ) + 3 6 2 0 × a ( S ) + 3 6 6 × a ( L ) This gives us, by plugging the apropriate values, a final result of 4225/7744 or 54.558%
worth reading, very nice !!
.we call the chance of Ag winning is S His chance of winning after rolling 6/8 is x His chance of winning after rolling 7 is y His chance of winning after rolling 6/8 AND a 7 is z we have these equations: z=5/36 + 25/36z y=10/36z + 20/36y x=5/36 + 6/36z + 25/36x S = 10/36x + 6/36y + 20/36 S solving these yields: z=5/11 y=25/88 x=85/121 S=4225/7744~54.558%
We know that we can a roll a 7 with two dice in 6 ways. While a 6 and an 8 both can be rolled in 5 ways. Yet the probability of rolling both a 6 and an 8 before throwing two 7's is higher. Lets see why...
The basic reason is that the order for getting a 6 or an 8 does not matter. The 6 - 8 combo is a favorite at the outset because there are 5+ 5 = 10 ways of getting either a 6 or an 8, whilst there are only 6 ways of getting a 7.
There are three ways that 6 and a 8 appear before two 7's.
1) Both 6 and a 8 appear before even one 7.
Now there are 10 out of 16 ways that either a 6 or an 8 appears first before a 7 because you don't mind either of them appearing.
Having got either of them, the chance of success, that is of getting the other number is 5/11 because now we specifically need either 6 or 8, whatever the case may be. (Remember the other numbers are disregarded when they are thrown)
Probability = 50/176
2) Either a 6 or 8 appears, then we hit a 7, then we throw the other number(6/8) before a second 7 appears.
10/16 chances of getting either 6 or 8 first.
6/11 chances that now a 7 comes up.
5/11 chance that the required relevant number, either 6 or 8 whichever is needed.
Probability = 300/1936
3) Finally 6, 8 appears after we throw the first 7.
6/16 chance of the first number being 7
10/16 chance of either 6 or 8
5/11 chance of the other required number of the two.
Probability = 300/2816
Adding up all these probabilities = 54.558 % !
Lets also check if the converse is correct.
Satvik wins in the 3 scenarios. Lets call rolling a 6 or 8 as Failure F
1) 77F
6/16 chances of rolling a 7
6/16 chances of rolling a 7
Probability = 36/256
2) 7F7
6/16 chances of getting a 7
10/16 chances of getting either 6 or 8
6/11 chances of getting a 7
Probability = 360/2816
3) F77
10/16 chances of of getting a 6/8
6/11 chances of a 7
6/11 chances of a 7
Probability = 360/1936
Adding them all together Percentage probability = 45.442 %
Combined total = 54.558 + 45.442 =100 %