did i miss something XD (try this)
A solid metallic sphere of mass and radius is free to roll (without sliding) over the inclined surface of a wooden wedge of equal mass . Wedge lies on a smooth horizontal floor. When the system is released from rest, find the ratio , here is the friction between the sphere and the wedge.
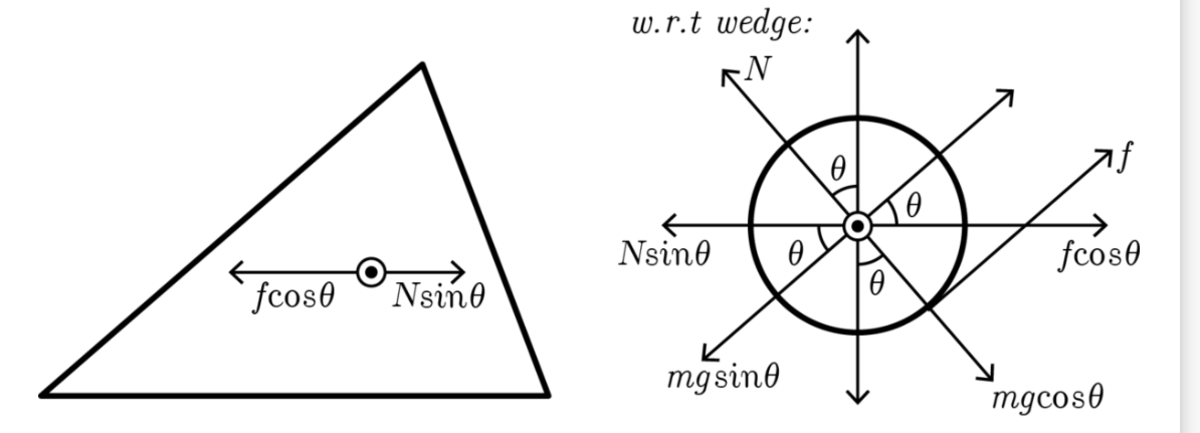
The wedge is a right triangle
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
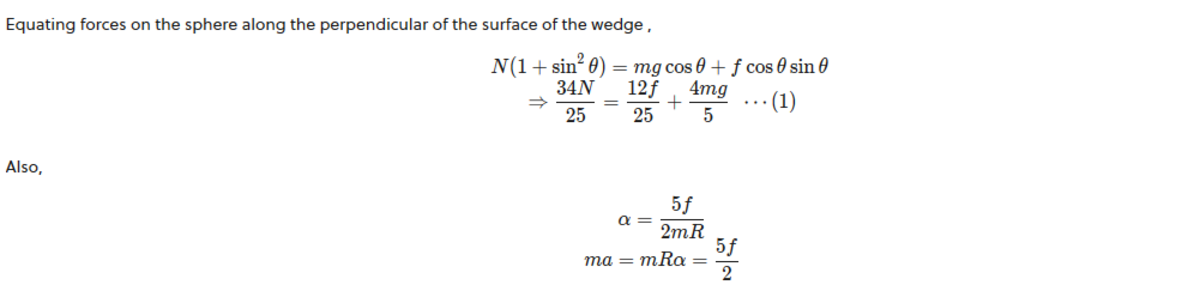
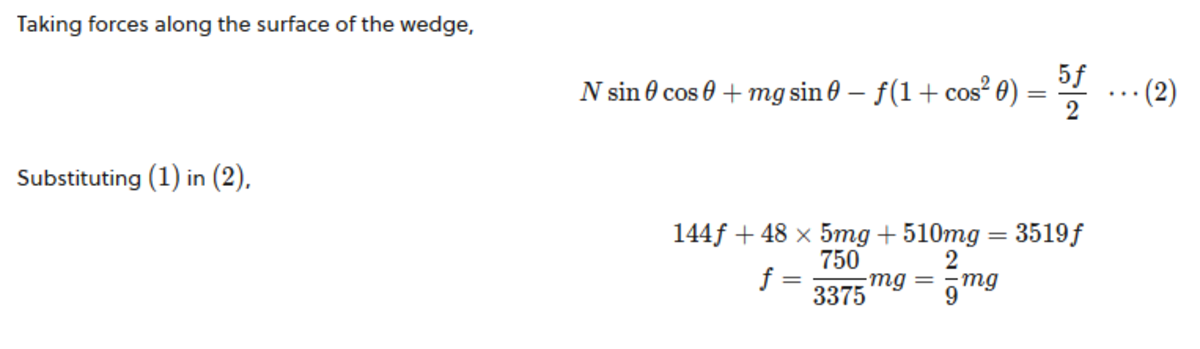
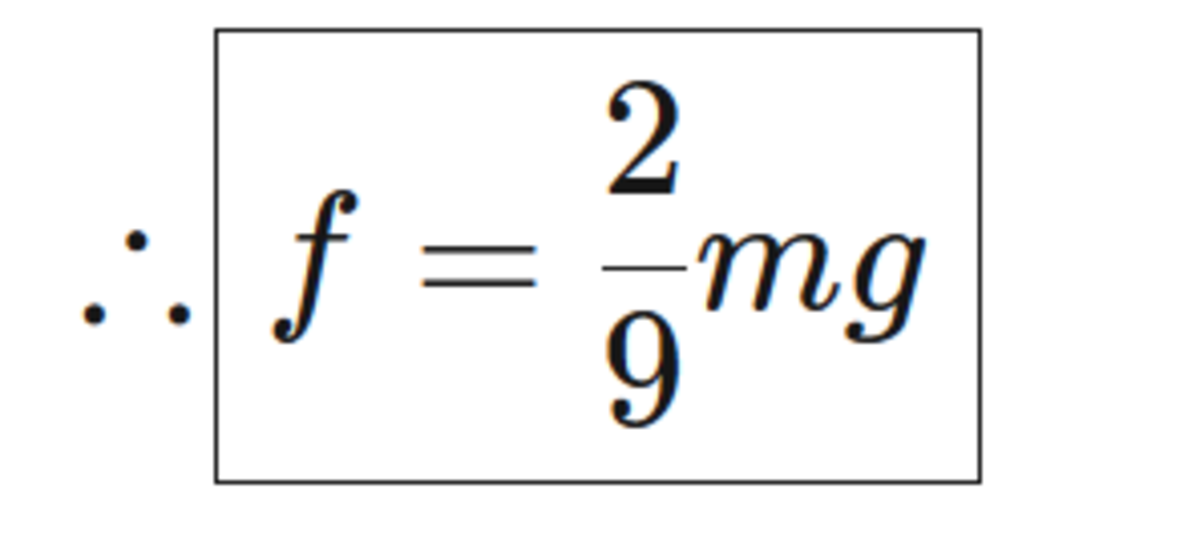
The force m a 1 acting on the sphere is a pseudo force.
The equations governing the motion of the sphere and wedge are:
m g + N 2 cos θ + f sin θ = N 1 … ( 1 ) N 2 sin θ − f cos θ = m a 1 … ( 2 ) m g cos θ = N 2 + m a 1 sin θ … ( 3 ) m a 1 cos θ + m g sin θ − f = m a 2 … ( 4 ) f R = ( 5 2 m R 2 ) α … ( 5 ) a 2 = R α … ( 6 )
Equation 1 balances forces along the vertical for the wedge.
Equation 2 is the application of Newton's 2nd law for the wedge along the horizontal.
Equation 3 is a force balance in a direction perpendicular to the incline for the sphere.
Equation 4 is the application of Newton's 2nd law for the sphere along the incline.
Equation 5 is the torque equation τ = I α about the COM of the sphere.
Equation 6 is the pure rolling constraint.
Taking cos 3 7 o = 0 . 8 and solving the six equations in six unknowns gives:
f = 9 2 m g N 2 = 3 2 m g
The resultant force between the wedge and the sphere is:
F = f 2 + N 2 2
Apologies for the messy diagram. I have denoted f as the friction force between the sphere and the wedge.