I just love primes!
Number Theory
Level
2
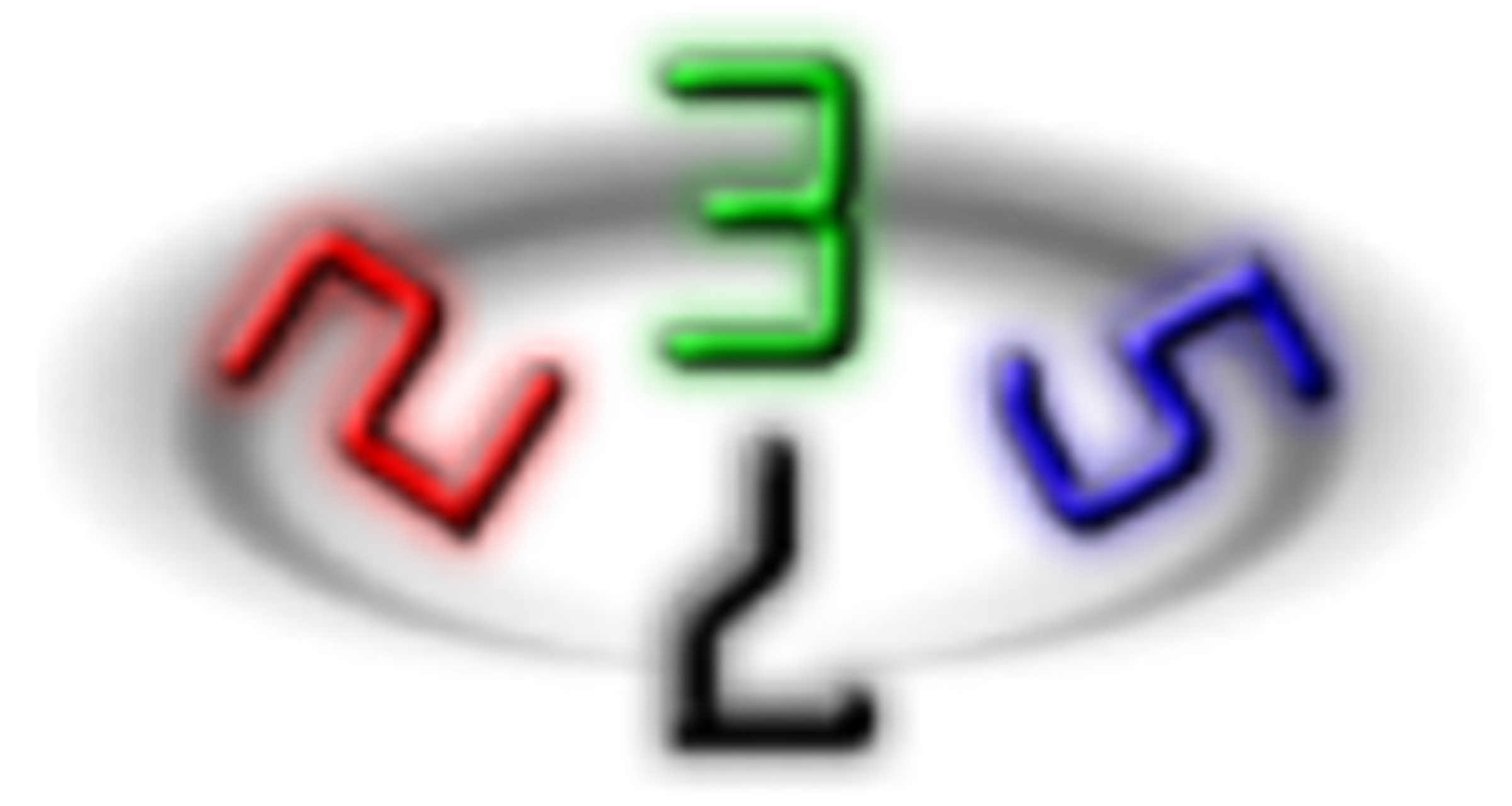
What is the smallest prime number that contains all the prime digits ?
The answer is 2357.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
This is the 3rd Smarandache-Wellin Prime, as in 2 , 2 3 , 2 3 5 7 , which is a prime number formed by concactenating successive primes. The 4th one is
2 3 5 7 1 1 1 3 1 7 1 9 2 3 2 9 3 1 3 7 4 1 4 3 4 7 5 3 5 9 6 1 6 7 7 1 7 3 7 9 8 3 8 9 9 7 1 0 1 1 0 3 1 0 7 1 0 9
1 1 3 1 2 7 1 3 1 1 3 7 1 3 9 1 4 9 1 5 1 1 5 7 1 6 3 1 6 7 1 7 3 1 7 9 1 8 1 1 9 1 1 9 3 1 9 7 1 9 9 2 1 1 2 2 3 2
2 7 2 2 9 2 3 3 2 3 9 2 4 1 2 5 1 2 5 7 2 6 3 2 6 9 2 7 1 2 7 7 2 8 1 2 8 3 2 9 3 3 0 7 3 1 1 3 1 3 3 1 7 3 3 1 3 3 7
3 4 7 3 4 9 3 5 3 3 5 9 3 6 7 3 7 3 3 7 9 3 8 3 3 8 9 3 9 7 4 0 1 4 0 9 4 1 9 4 2 1 4 3 1 4 3 3 4 3 9 4 4 3 4 4 9
4 5 7 4 6 1 4 6 3 4 6 7 4 7 9 4 8 7 4 9 1 4 9 9 5 0 3 5 0 9 5 2 1 5 2 3 5 4 1 5 4 7 5 5 7 5 6 3 5 6 9 5 7 1 5 7 7
5 8 7 5 9 3 5 9 9 6 0 1 6 0 7 6 1 3 6 1 7 6 1 9 6 3 1 6 4 1 6 4 3 6 4 7 6 5 3 6 5 9 6 6 1 6 7 3 6 7 7 6 8 3 6 9 1
7 0 1 7 0 9 7 1 9
This happens because the larger a random number is, the less likely that it's a prime. So, a lot of primes have to keep being added until there is a "hit".
Meanwhile, of the 2 4 possible permutations of 2 , 3 , 5 , 7 , exactly 8 are primes
2 3 5 7 , 2 7 5 3 , 3 2 5 7 , 3 5 2 7 , 5 2 3 7 , 5 2 7 3 , 7 2 5 3 , 7 5 2 3