Did you know the basics of Limits.
Calculus
Level
4
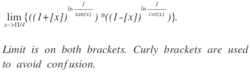If value of above limit is K/20. Find K.
The answer is 20.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
This is a very easy problem involving basics of Limit.
The value of k is 20.
As we approach to pi/4, [x] becomes 0. So the quantities in both brackets become exactly 1.
Now whatever be in the power, the answer of above limit will be one.
Some of you might be confusing it with "1 raised to the power infinity" form. In that case quantity inside the bracket doesn't becomes exactly 1. But, it tends towards 1. Now, the problem arises here. For example, if we say that it is tending 1 from left hand side i.e it's actual value (not limiting value) will be less than 1. In this case, that number raised to the power infinity will become 0. But if we say that it tends towards 1 from RHS, then using same concept it becomes infinity. Since, we are not confirmed from which side it is tending to 1, We say it is indeterminate form .
But, here Quantity in bracket becomes exactly 1. So, it doesn't matter to which power it is raised, it will always be 1.
Same is the case with any indeterminate form. If someone asks you that what is value of [|x|]/x if x is tending towards zero, then answer will be zero. Because numerator becomes exactly zero and denominator is a finite number tending towards zero. It is not a indeterminate form.