Did you say scale it?
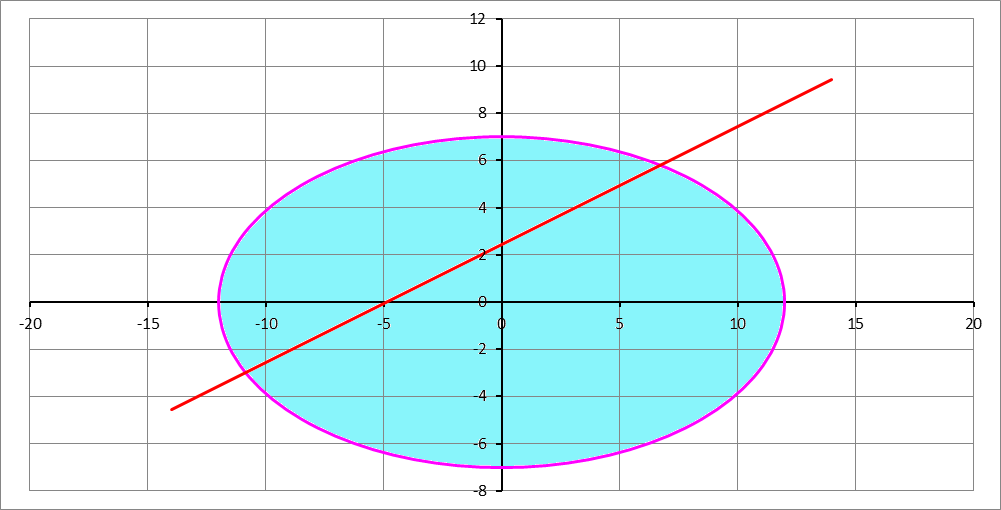
Consider the elliptical area (shaded in light blue) in the figure above. It is given by
a 2 x 2 + b 2 y 2 ≤ 1
where a = 1 2 , and b = 7 .
I want to draw a straight line whose equation is y = 2 1 x + y 0 that will cut through the elliptical area dividing it into two parts, with the upper part being one third of the total elliptical area. Find the y-intercept y 0 , and input ⌊ 1 0 5 y 0 ⌋ as your answer.
The answer is 244255.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
We start off by scaling the ellipse into the unit circle, by defining the image of ( x , y ) to be ( x ′ , y ′ ) with x ′ = a x ,and y ′ = b y .
The image of the line becomes: b y ′ = 2 1 a x ′ + y 0
Now this line is to be distant from the origin a distance D , such that the area of the circle above y = D is 3 1 of the unit circle area.
Let θ = 2 cos − 1 ( D ) , then the upper area is = 2 1 ( θ − sin ( θ ) ) .
Hence , 3 1 π = 2 1 ( θ − sin ( θ ) ) = 2 1 ( 2 cos − 1 ( D ) − sin ( 2 cos − 1 ( D ) ) )
We can find D numerically, by a suitable numerical method, such as Newton's method. To use this method, we
define the function f ( x ) = 2 1 ( 2 cos − 1 ( x ) − sin ( 2 cos − 1 ( x ) ) ) − 3 1 π , and we want the root of this function.
Newton's iteration, is given by x n + 1 = x n − f ′ ( x n ) f ( x n ) , where the derivative of our function is f ′ ( x ) = 2 1 ( 1 − x 2 − 2 − cos ( 2 cos − 1 ( x ) ) ⋅ 1 − x 2 ( − 2 ) )
This can be simplified and re-arranged into f ′ ( x ) = − 2 1 − x 2
Putting it all together and using any programming environment or a standard spreadsheet like Microsoft Excel, we can implement the Newton Iteration. I have taken the initial guess x 0 = 0 . 5 . You'll note that the iterations converge very quickly to our sought solution and we have the desired solution D = 0 . 2 6 4 9 3 2 0 8 5
Now we are ready to continue the solution. Recall that our line is given by b y ′ = 2 1 a x ′ + y 0
Its distance from the origin is given by: D = b 2 + 4 a 2 y 0
Thus y 0 = D b 2 + 4 a 2 = 0 . 2 6 4 9 3 2 0 8 5 4 9 + 4 1 4 4 = 2 . 4 4 2 5 5 3 1 3
This makes the answer ⌊ 1 0 5 y 0 ⌋ = 2 4 4 2 5 5
I proceeded in three steps. Having limited time, I "cheated" and left the numerical work in Step 1 to the computer.
First find a line x = a that cuts the area of the unit circle in a ratio of 2:1. Solving ∫ 0 a 1 − x 2 d x = 2 1 ( a 1 − a 2 + arcsin a ) = 1 2 π numerically gives a ≈ 0 . 2 6 4 9 3 2 0 8 .
Second, find a line y = 7 6 x + b that cuts the area of the unit circle in a ratio of 2:1. We want the line's distance from the origin to be a , so b = a 1 + ( 7 6 ) 2 .
Finally, we are scaling our line by a factor of 12 horizontally and by a factor of 7 vertically, x ′ = 1 2 x and y ′ = 7 y , to take the form y ′ = 2 x ′ + 7 b with y 0 = 7 b = 8 5 a ≈ 2 . 4 4 2 5 5 3 1 .
The required answer is 2 4 4 2 5 5