Diet Tetris (Take 2)
Using any rotation of the L-shape and straight piece below:
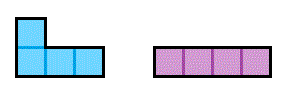
there are exactly 5 ways that a 2 × 8 box can be completely tiled:
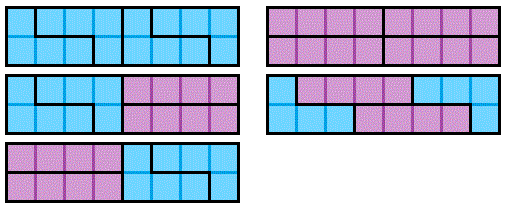
Find the number of ways a 2 × 1 0 0 box can be completely tiled by using any rotation of the L-shape and straight piece above.
The answer is 20365011074.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
Let
f
(
n
)
be the number of fully tiled 2 x 4n boxes and
g
(
n
)
the number of "overtiled" 2 x 4n boxes, such as this one (overtiled 2 x 4 box)
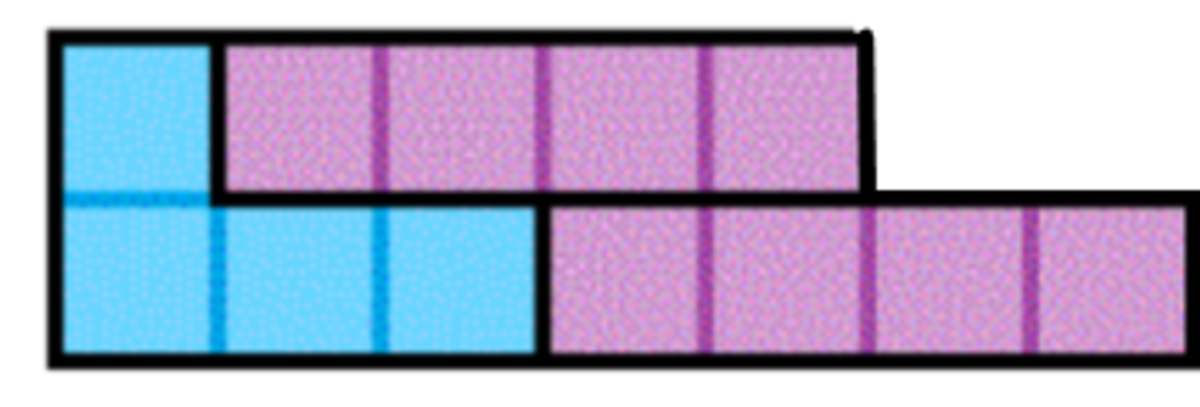 Then for each fully tiled 2 x 4n box we can add one purple
or
one blue 2 x 4 block to get a fully tiled 2 x 4(n + 1) box. Also, for each overtiled 2 x 4n box we can add one L - shape to get a fully tiled 2 x 4(n+1) box. The recurrence relation for
f
(
n
)
is therefore
f
(
n
+
1
)
=
2
f
(
n
)
+
g
(
n
)
. Another equation is for overtiled boxes, which can be made either by adding an L - shape after a fully tiled sequence
or
a Z - shape (two misaligned purple bars) after an overtiled sequence. Thus, second equation is
g
(
n
+
1
)
=
f
(
n
)
+
g
(
n
)
. Initial conditions are
f
(
1
)
=
2
and
g
(
1
)
=
1
. Wolfram Alpha successfully solves such systems (even the free version). The answer is
f
(
2
5
)
=
2
0
3
6
5
0
1
1
0
7
4
.
Then for each fully tiled 2 x 4n box we can add one purple
or
one blue 2 x 4 block to get a fully tiled 2 x 4(n + 1) box. Also, for each overtiled 2 x 4n box we can add one L - shape to get a fully tiled 2 x 4(n+1) box. The recurrence relation for
f
(
n
)
is therefore
f
(
n
+
1
)
=
2
f
(
n
)
+
g
(
n
)
. Another equation is for overtiled boxes, which can be made either by adding an L - shape after a fully tiled sequence
or
a Z - shape (two misaligned purple bars) after an overtiled sequence. Thus, second equation is
g
(
n
+
1
)
=
f
(
n
)
+
g
(
n
)
. Initial conditions are
f
(
1
)
=
2
and
g
(
1
)
=
1
. Wolfram Alpha successfully solves such systems (even the free version). The answer is
f
(
2
5
)
=
2
0
3
6
5
0
1
1
0
7
4
.
Let t ( n ) be the number of ways of tiling a 4 n × 2 box. Say a tiling has a "vertical break" if we can split it into a tiling of a 4 k × 2 box and a 4 ( n − k ) × 2 box, where 0 < k < n , without cutting a tile. A couple of observations first:
1) There are two ways to tile a 4 × 2 box with no vertical breaks 2) There is a unique way to tile a 4 n × 2 box with no vertical breaks for n > 1 (see the last picture in the question for an example)
From this we can build a recurrence for t ( n ) : there is 1 way to tile the whole box with no vertical breaks. There are 2 t ( n − 1 ) tilings in which the first vertical break from the left creates a 4 × 2 box. Then there are t ( n − k ) tilings whose first vertical break from the left creates a 4 k × 2 box, where 1 < k < n .
Putting all this together, we have t ( 1 ) = 2 , t ( 2 ) = 5 and t ( n ) = 1 + 2 t ( n − 1 ) + k = 2 ∑ n − 1 t ( n − k )
or, re-indexing the sum, t ( n ) = 1 + 2 t ( n − 1 ) + k = 1 ∑ n − 2 t ( k )
Also, t ( n + 1 ) = 1 + 2 t ( n ) + k = 1 ∑ n − 1 t ( k ) so that t ( n + 1 ) − t ( n ) t ( n + 1 ) = 2 t ( n ) − t ( n − 1 ) = 3 t ( n ) − t ( n − 1 )
This is enough to find the answer; we get t ( 2 5 ) = 2 0 3 6 5 0 1 1 0 7 4 .
But there's more! The first few values of t ( n ) are 2 , 5 , 1 3 , 3 4 , 8 9 , … - which are all Fibonacci numbers (in fact the sequence is every other Fibonacci number).
If F n is the n th Fibonacci number, we have F n F n + 1 F n + 2 = F n − 1 + F n − 2 = F n + F n − 1 = F n + 1 + F n
By eliminating F n − 1 and F n + 1 we find F n − 1 F n + 1 F n + 2 = F n − F n − 2 = F n + ( F n − F n − 2 ) = 2 F n − F n − 2 = ( 2 F n − F n − 2 ) + F n = 3 F n − F n − 2
which - together with the first two values of t ( n ) - proves that t ( n ) = F 2 n + 1 . So in particular t ( 2 5 ) = F 5 1 .
Can anyone provide a more direct explanation for why Fibonacci numbers appear here? It's interesting that the number of ways of tiling a n × 2 box with dominoes is also a Fibonacci number.
Log in to reply
Not sure if it is what you are looking for, but I posted my solution that explains a little bit about why Fibonacci numbers appear in this problem.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 |
|
Filling in pieces from left to right, there are only 4 different combinations that can be added to completely fill the grid:

If the rightmost piece ends evenly, A or D can be used next, but if the rightmost piece ends unevenly, B or C can be used next. If A is used next then the rightmost number of pieces increases by 3 , if B is used next then the rightmost number of pieces increases by 1 , if C is used next then the rightmost number of pieces increases by 4 , and if D is used next then the rightmost number of pieces also increases by 4 .
If A n is the number of ways a sequence with a length of n ends in A , B n is the number of ways a sequence with a length of n ends in B , C n is the number of ways a sequence with a length of n ends in C , and D n is the number of ways a sequence with a length of n ends in D , we have the following relationships:
A n + 3 = B n + D n
B n + 1 = A n + C n
C n + 4 = A n + C n
D n + 4 = B n + D n
where A 3 = 1 , B 4 = 1 , C 3 = 0 , and D 4 = 1 .
With a little manipulation, B n + 1 = A n + C n = ( B n + D n ) + ( A n − 1 + C n − 1 ) = B n + D n + B n = B n + D n + 4 , or B n = D n + 4 + B n .
Using D 4 = 1 , B 4 = 1 , D n + 4 = B n + D n , and B n = D n + 4 + B n , the first few terms are ( D 4 , B 4 , D 8 , B 8 , D 1 2 , B 1 2 . . . ) = ( 1 , 1 , 2 , 3 , 5 , 8 , . . . ) = ( F 1 , F 2 , F 3 , F 4 , F 5 , F 6 , . . . ) , the Fibonacci sequence. Therefore, D n = F 2 1 n − 1 and B n = F 2 1 n for n values that are multiples of 4 .
A completed grid will end with either B or D for a total of S n = D n + B n = F 2 1 n − 1 + F 2 1 n = F 2 1 n + 1 ways.
Therefore, for a 2 × 1 0 0 grid, there are S 1 0 0 = F 2 1 ⋅ 1 0 0 + 1 = F 5 1 ways to fill it. Using Binet's formula, that means there are F 5 1 = 5 1 ( ( 2 1 + 5 ) 5 1 − ( 2 1 − 5 ) 5 1 ) = 2 0 3 6 5 0 1 1 0 7 4 ways to fill the 2 × 1 0 0 grid.
Aha, so there's the Fibonacci relation. Silly question perhaps, but what exactly do the A n denote? (I think you missed something defining these)
Log in to reply
It's the number of ways a sequence with a rightmost length of n ends in A . I'll edit that in.
Thank you! Until this moment I don't know that we can calculate the nth term of the Fibonacci sequence.
Tiling problems are related to Fibonacci sequences and recursion, and hence are very suitable for the application of dynamic programming.
First, think of the 2 × 1 0 0 box as a collection of 2 5 small boxes of size 2 × 4 . We will start tiling from the leftmost box and consider one box at a time. We define the number of ways the n t h box can be filled with no overreach as j a r [ n ] [ 0 ] and the number of ways it can be filled with overreach as j a r [ n ] [ 1 ] .
Whenever we try to fill a particular box (say, ( n + 1 ) t h box), we can have 2 possible initial states. In one state, the box will be empty initially. In the other case, it will have overreach from the previous box (in this case, the n t h box). So, in how many ways can we fill the ( n + 1 ) t h box?
If we want to fill the box with no overreach, we can do it in 2 ⋅ j a r [ n ] [ 0 ] + j a r [ n ] [ 1 ] ways. And, if we want fill it with overreach, the number of ways will be j a r [ n ] [ 0 ] + j a r [ n ] [ 1 ] . Hence, we get the following recursive relations.
j a r [ n + 1 ] [ 0 ] = 2 ⋅ j a r [ n ] [ 0 ] + j a r [ n ] [ 1 ] j a r [ n + 1 ] [ 1 ] = j a r [ n ] [ 0 ] + j a r [ n ] [ 1 ]
with the initial conditions
j a r [ 0 ] [ 0 ] = 1 j a r [ 0 ] [ 1 ] = 0
Here, what we want to find is j a r [ 2 5 ] [ 0 ] .
N.B. I implemented the 2d array in a 1d list.