Difference fun

Logic Level 2

$\Large \square - \square$

The above 2 boxes are to be filled in with 2 distinct integers between 1 and 100 (inclusive).

If the resultant number is positive but no more than 10, how many pairs of such integers can there be?

The answer is 945.

3 solutions

Spandan Senapati
Mar 17, 2017

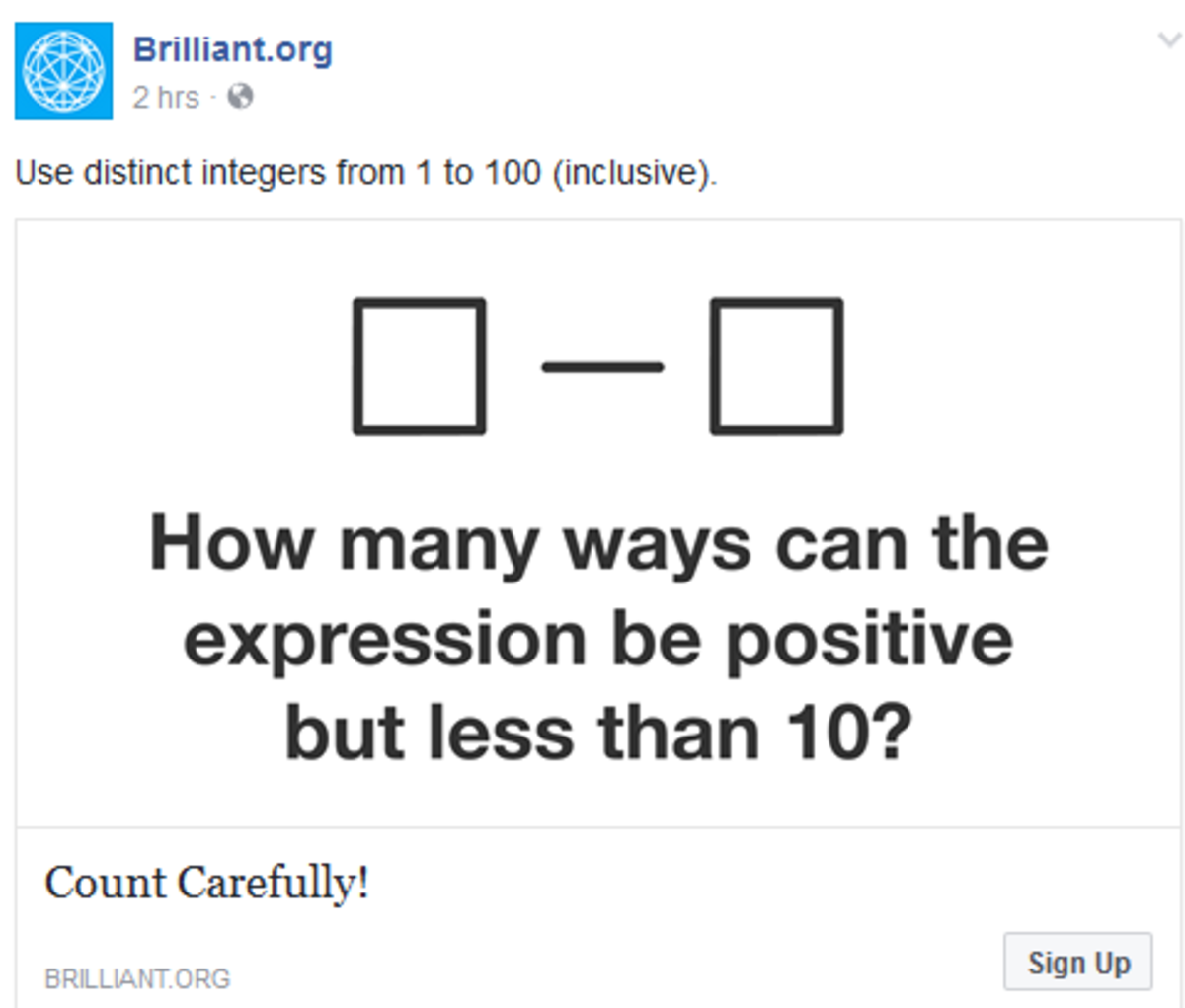
A simplistic approach Let's consider the difference as $1$ then we get $99$ pairs.If the difference is $2$ then we get $98$ pairs and similarly proceeding if the difference is $10$ we have $90$ pairs.So the Ans is $90+91+.....99=90*10+(1+2+3+4+5......9)=900+(9*10/2)=945$

Yes this is a nice alternative solution to this problem and I feel rather easy one

Om Adarsh - 4 years, 2 months ago

Are bhai again active??

Spandan Senapati - 4 years, 2 months ago

Ya this was easy one.I solved the q orally

Spandan Senapati - 4 years, 2 months ago

Hahaa if I vl be active u vl get scolding yahooooo bravo

Om Adarsh - 4 years, 2 months ago

Om Adarsh
Mar 15, 2017

Let the choosen integers be x and y Let there be m integers before x, n integers between x and y and p integers after y This implies m+n+p=98 where m>=0,n>=10,p>=0 Now if we consider the choices where difference is atleast 11 no of solutions is 88+3-1c2=4005 The number of ways in which n is less than 10 is 100c2-4005=945 Ans: 945

John Miller
May 5, 2017

There are actually two problems here -- the one as stated on Brilliant.org and the one as stated on Facebook, which reads,

My solution is that someone should proofread the Facebook posting to ensure it's the same as the actual problem on Brilliant.

Difference fun

The answer is 945.

3 solutions

0 pending reports