Difference in circles' areas

Geometry Level 2

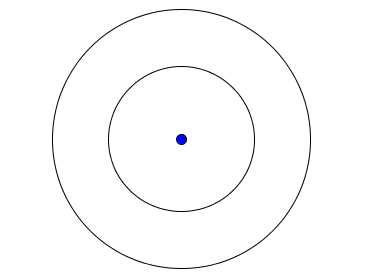
Ajay learned that area of a circle is $\pi$ times the square of it's radius. He calculated the difference in area of the above circles as $49\pi$ when the difference in the radii of the above circles is given $7$ . Is he right?

No Yes

2 solutions

Anandmay Patel
Aug 21, 2016

According to the question,49(pi)=(pi)[R^2-r^2],where R and r are the radii of the big and small circle respectively.The equation is equivalent to:49=[R^2-r^].But,R-r=7(given),results in R+r=7.But R+r and R-r can never be simultaneously zero,as it results in either R or r = 0,which can never happen as R and r are the radii of 2 cicles.

But, a point is nothing but a circle with zero radius. It is possible. You can have R=7 and r=0.Its possible. Answer should be YES.

A Former Brilliant Member - 2 years, 7 months ago

@A Brilliant Member At that point it's just a plain old regular circle, not the figure shown in the problem.

Deva Craig - 1 year, 9 months ago

Chew-Seong Cheong
Aug 20, 2016

Since the difference in area of the big circle and small circle is $49\pi$ , this means that the areas of the small and big circles must be $\pi$ and $50 \pi$ respectively. Therefore, the radii of the small and big circles are $1$ and $\sqrt{50}$ respectively and the difference is $\approx 6.071067812$ . The answer is $\boxed{No}$ .

Why specifically $\pi$ and $50 \pi$ would be the only two possible areas whose difference gives $49 \pi$ ? Is there an intuition that $n \pi - m \pi = 49 \pi$ where $m$ and $n$ are positive integers, will give the maximum value of $\sqrt{n} - \sqrt{m}$ for $n=50$ and $m=1$ ?

Tapas Mazumdar - 4 years, 3 months ago

Difference in circles' areas

2 solutions

0 pending reports