Difference of Areas of an ellipse and a curve
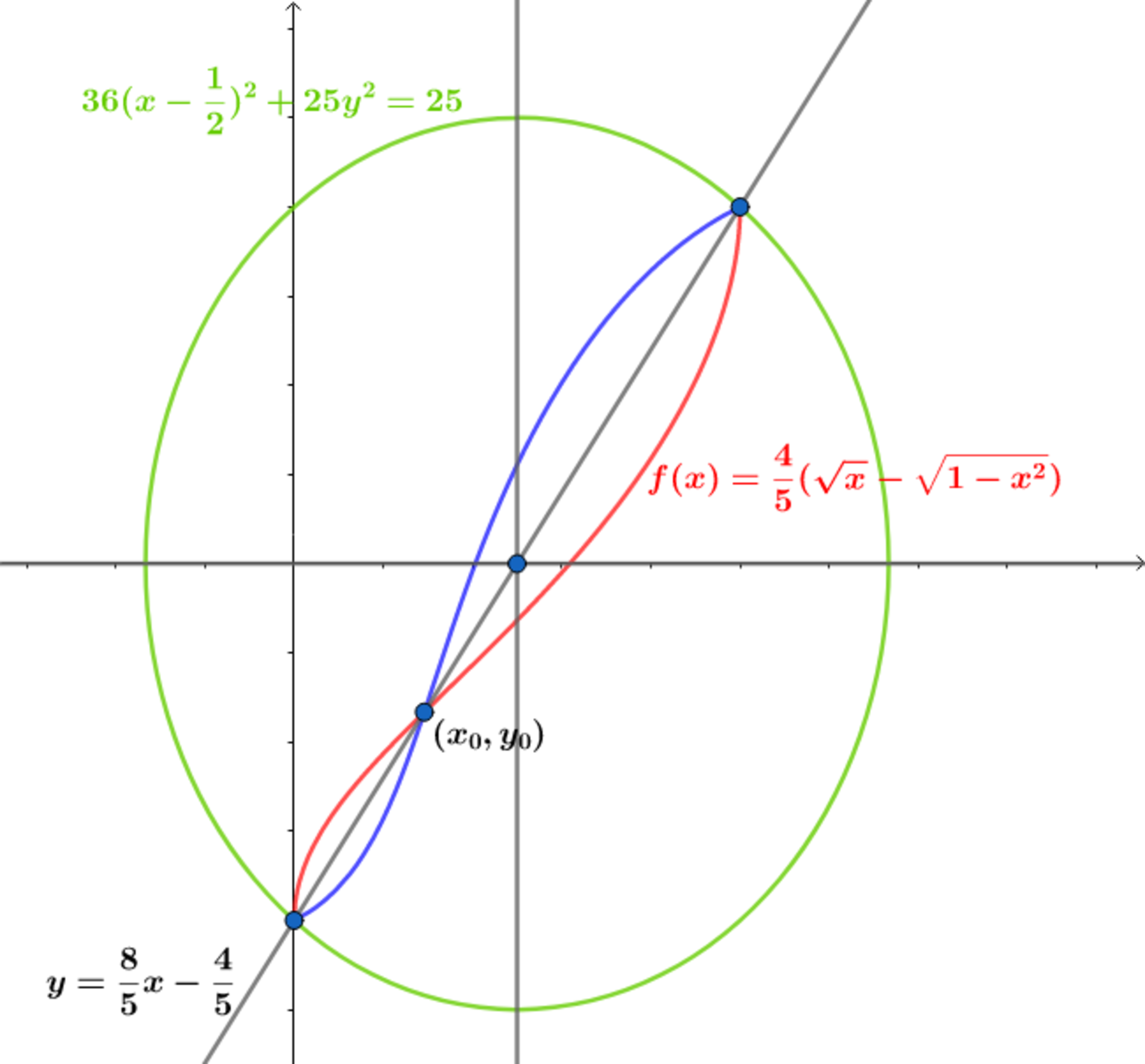
When the curve is reflected about the line a closed curve is formed.
Find the area of the closed curve formed above.
Find the area of the ellipse .
Find the difference to four decimal places.
:
The answer is 2.3508.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
To find ( x 0 , y 0 ) :
5 4 ( x − 1 − x 2 ) = 5 4 ( 2 x − 1 ) ⟹ x − 2 x 1 − x 2 + 1 − x 2 = 4 x 2 − 4 x + 1 ⟹ 5 x − 5 x 2 = 2 x 1 − x 2
⟹ 2 5 x 2 ( 1 − 2 x + x 2 ) = 4 x − 4 x 3 ⟹ 2 5 x 4 − 5 0 x 3 + 2 5 x 2 = 4 x − 4 x 3 ⟹ x ( 2 5 x 3 − 4 6 x 2 + 2 5 x − 4 ) = 0 ⟹
x ( x − 1 ) ( 2 5 x 2 − 2 1 x + 4 ) = 0 ⟹ x = 0 , x = 1 , x = 5 0 2 1 ± 4 1 .
From the graph above two points of intersection are ( 1 , 5 4 ) and ( 0 , 5 − 4 ) . Since there are only three points of intersection ⟹ only one of the values of x = 5 0 2 1 ± 4 1 are valid.
Choosing x 0 = 5 0 2 1 − 4 1 ⟹ y ( x 0 ) = f ( x 0 ) = 1 2 5 − 4 ( 4 + 4 1 ) .
A 1 ∗ = 2 ∫ x 0 1 ( y − f ( x ) ) d x = 5 8 ∫ x 0 1 ( 1 − x 2 − x + ( 2 x − 1 ) ) d x .
Let x = sin ( θ ) ⟹ d x = cos ( θ ) ⟹ A 1 ∗ = 5 8 ( 4 π − 2 1 arcsin ( x 0 ) − 2 1 x 0 1 − x 0 2 − 3 2 + 3 2 x 0 2 3 − x 0 2 + x 0 )
In a similar fashion:
A 2 ∗ = 2 ∫ 0 x 0 ( f ( x ) − y ) d x = 5 8 ∫ 0 x 0 ( − 1 − x 2 + x − 2 x + 1 ) d x =
5 8 ( 2 − 1 arcsin ( x 0 ) − 2 1 x 0 1 − x 0 2 + 3 2 x 0 2 3 − x 0 2 + x 0 ) .
The desired area A 1 = A 1 ∗ + A 2 ∗ = 5 8 ( 4 π − arcsin ( x 0 ) − x 0 1 − x 0 2 − 3 2 + 3 4 x 0 2 3 − 2 x 0 2 + 2 x 0 ) ≈ . 2 6 7 1 9 3 9
The ellipse 3 6 ( x − 2 1 ) 2 + 2 5 y 2 = 2 5 ⟹ y = 5 1 2 5 − 3 6 ( x − 2 1 ) 2 , where 3 − 1 ≤ x ≤ 3 4 ⟹ A 2 = 5 2 ∫ 3 − 1 3 4 2 5 − 3 6 ( x − 2 1 ) 2 .
Letting 6 ( x − 2 1 ) = 5 sin ( θ ) ⟹ A 2 = 6 5 ∫ 2 − π 2 π ( 1 + cos ( 2 θ ) ) = 6 5 ( θ + 2 1 sin ( 2 θ ) ) ∣ 2 − π 2 π = 6 5 π ⟹
A 2 − A 1 ≈ 2 . 3 5 0 8