Different Area
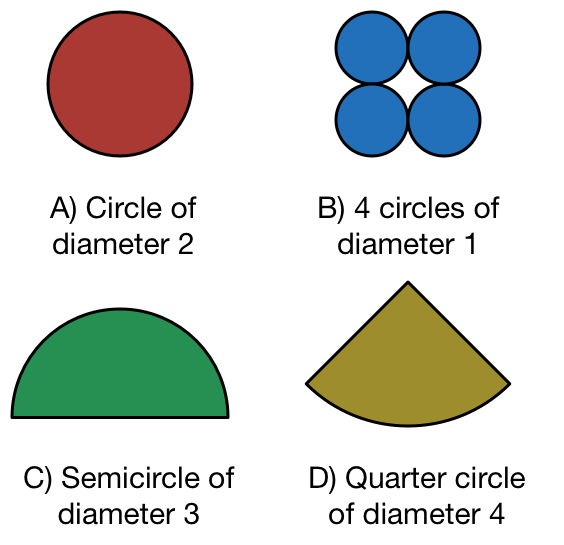 Which of these shapes has an area that is different from the rest?
Which of these shapes has an area that is different from the rest?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
18 solutions
Moderator note:
Yes this is the standard approach.
Bonus question : Is there an odd one out for their respective perimeters?
I like the bonus question of Brilliant.
For that we should know the perimeter formulas of these shapes.
1}Circle's perimeter formula: 2πr
2}4 times the Circle's perimeter formula:
8πr
3}Semicircle's perimeter formula: r(π+2)
4}Quarter circle's perimeter formula:
(πr)/2 +2r
•°• Cancel π and r from each the
expression as π and r is common.
We get :
1}(2πr)/(πr)=2
2} (8πr)/(πr)=8
3}[r(π+2)]/πr=(πr+2r)/πr=(πr/πr)+(2r/ πr)=
4/π
4}[(πr)/2+2r]/πr=(πr/2πr)+(2r/πr)=
(π+4)/2π
Now let's cancel 2 and it's multiples by 2
1}2/2=1
2}8/2=4
3}(4/π)/2=4/2π=2/π
4}[(π+4)/2π]/2=(π+4)/4π
Now put π it's value which is 22/7
Then the value should be:
1}1=1
2}4=4
3}2/π=2/(22/7)=11/7=1(4/7)
4}(π+4)/4π=[(22/7)+4/4(22/7)]=
(50/7)/(88/7)= 25/44
So, no we can arrange it like this:
25/44<1<1(4/7)<4
It spells:
25/44is smaller than 1 which is smaller than 1(4/7) which is smaller than 4.
Therefore, there is no odd one out because there is no relationships between them.
Python 2.7:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 |
|
Bonus points for the cool python script :)
Insightful and analytical! I love that you incorporate your motivation and reasoning behind every step in your solution. Thank you.
Another way to think of this question is which number given is different? A semicircle of radius 3 is an odd numbered radius. If I square the radius (following the formula for area of a circle), I get an odd number (9). Then because it's a semicircle, its area is half that number times pi. This yields a decimal number for the area.
When you look at the other choices, they all deal with either even numbers or 1. 1 has a special property that anything multiplied by 1 will be unchanged, meaning that 1^2 is still 1 and when an even number is multiplied by 1, it will remain an even number. Also, a whole number will remain a whole number when multiplied by 1.
With this knowledge in mind, we can discern quite easily that none of the other areas will be a decimal number multiplied by pi. Therefore due to the question's parameters, the shape with the different area (if there is one, which there is) must be C, a semicircle of radius 3.
One final way to think about it is do two choices have the same area with another having a different area? If yes, then we need not bother worrying about the fourth choice, as the answer will be the choice with the different area.
C has the area of 3.53 rest are having 3.14
Moderator note:
And how would you know that?
Area of a circle = pi.r^2
Area of a circle with diameter 2 = pi.1^2 = pi
Area of 4 circles with diameter 1= 4.pi.0,5^2=pi
Area of quarter circle with Diameter 4 = 1/4.pi.2^2=pi
Area of semicircle with diameter 3 = 1/2.pi.1,5^2= 1,125.pi
in a),b),d)area=1 * (pie)
and
c)having area=1.125 * (pie)
Moderator note:
How would you know that? Pie?
The other three are red, blue, and yellow, which are primary colors. C is green, which is not a primary color, so it is different.
Furthermore, A, B, and D can fit inside a square with side length 2 while C cannot.
Also, A is 1 circle and 1 = 1 , B is 4 circles and 4 = 2 , C is half a circle and 1 / 2 is not rational, and D is 1/4 of a circle and 1 / 4 = 1 / 2 . Clearly C is the odd one out.
Finally, A, B, and D all have area π while C does not.
Moderator note:
Can you show the working for your (one right) solution?
Loved the way you arrived at an answer to 'Which of these is different from the rest?'
We knew area of circle is pie r square A) diameter is 2 thus radius is 1 . 1 square =1 B) diameter is 1 thus radius is 1/2 . 1/2 square is 1/4 *4 = 1 D) diameter is 4 thus radius is 2 and . 2 square is 4 *0.25 = 1 Where as C) diameter is 3 thus radius is 1.5 . 1.5 square * 0.25 = 1.125 Thus C) is different....
Pi x r squared. 1x1=1, .5x.5x4=1, 1.5x1.5/2=1.125, 2x2x.25=1 C is wrong answer.
Applying the basic rule for area we know that area of a circle is pi times the radius squared while that of a semi circle is jalf of pi tomes the radius squared and like so As pi will be in the area formula for all the shapes, this can be omitted (cancelled out). Thus, we have to find the circles with a different value for r^2. A) =1, B) =1, D) =1, However, C) =1.125 Hence C is the odd one out
Except semicircle ,each is having area pie(3.14) using formula of area of circle
Area of a circle is Pi r2, thus C equals 3.534 while A, B and C equals 3.141
A= 2pi R^2= 2pi
B= 4(2pi 1/2^2)= 2pi
C= 1/2 (2pi 3/2^2)= 9/4 pi
D= 1/4 ( 2pi 4/2^2)= 2 pi
The formula for area is pi* r^2. Not. 2 *pi * r^2.
We calculate areaof each,which by putting radius values in pi r2 is 3.14 in cases a ,b and d therefore figure 3 is different than others.ans
Just look at the diameters of all options, C is an oddball. So my thinking is that let's forget about the exact formula of calculating the area of a circle, the area of a circle has to do with its diameter, that is all we need to know. Comparing A to B, the diameter was halved (from 2 to 1), but the number of circles are quadrupled, so that should negate each other. Comparing A to D, the diameter was doubled (from 2 to 4), but the D was sliced into a quarter of a cirlcle, so that should negate each other too. In other words, between A to B and between A to D, it is a balanced play between the differences of diameters and whethe the number of circles is either multiplied by four (A to B) or divided by 4 (A to D). So that makes A, B, D the same in size. That leaves the option C, which has a diameter of 3, not a multiplication of 2 by any means. It has to be the oddball.
Hellooooooo ?
Ans C as π(1.5)^2÷2=3.5
A,B& D area are π, and c area is 1.125π. so c is different to others.
Moderator note:
Where's your working? Despite getting the right conclusion, you have calculated all the values wrongly. Can you recall the area of a circle?
Not to sound to pitiful, But how did everyone figure out the area of thee shapes
A) 2 x 2 x pi = 4 x pi.
B) 4 x 1x 1 x pi = 4 x pi.
C) 3 x 3 x pi x 1/2 = 9/2 x pi.
D) 4 x 4 x pi x 1/4 = 4 x pi.
=> The answer is C
Moderator note:
Are you sure about that? Recall the area of a circle is π r 2 with r as its radius, not its diamater.
The area of a circle is pi times the radius squared.
As pi will be in the area formula for all the shapes, this can be omitted (cancelled out). Thus, we have to find the circles with a different value for r^2.
A) 1 2 =1,
B) 0 . 5 2 × 4 =1,
D) 2 2 × 0 . 2 5 =1,
However,
C) 1 . 5 2 × 0 . 5 =1.125
Thus, the area of shape C is different