Different divisors gets the same remainder!
When 31513 and 34369 are each divided by a certain three-digit number, the remainders are equal. Find this remainder.
The answer is 97.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
15 solutions
Is there any chance of having different remainders when dividing the 5 digit number by the factors of their difference? If yes then how to know which remainder was the required one?
Log in to reply
For this problem, the given five-digit numbers happen to be 97 mod 2856, and so they are also 97 mod any three-digit factor of 2856. This is not true in general (consider 25150 and 26150, which leave both remainders of 50 mod 100 but also both 150 mod 200).
Why do they yield the same remainder?
Log in to reply
See Arjen's answer
Log in to reply
Gaussian Clocks (Modulo Arithmetic) - consider a standard clock. 3:00 is 12 oclock + 3 hours, the next time I am 3 hours after midday/midnight will be when the clocks have moved on by that same amount, i.e. 12 hours, 15:00, then 27:00 all these show as 3:00 on a 12 hour clock. This is modulo 12 arithmetic. The argument above is about a clock in which 2856 units later the hands are in the same place as 0. On this clock 31513 is 97 past the 0 as is 34369 as (31513 % 2856) is equal to (34369 % 2856) - here I am using a computer programmers common method of represent mod as %.
I 👍 your explanation. But prime factors of 2856 is 17, 7, 3, 2, 2, 2; i.e.: 2856 = 17 × 7 × 3 × 2 × 2 × 2. Here, 17 is the only number which when used as a divisor to the given numbers 31513 and 34369, gives same reminder as 12. The product of rest of the prime factors excluding 17 is 168; i.e. 7×3×2×2×2 = 168. Is there something to do with 17?
Log in to reply
It is correct also, but seems we cannot get remainder bigger than divisor: 9 7 > 1 7 , so get 9 7 ≡ 1 2 ( m o d 1 7 ) instead. Make sure to check question statement: 17 isn't a three-digit number :)
31513 is A prime numbe.34369 is a prime number,too.so it is impossible to find other numbers to devide 31513 & 34369 except 1 & themself.
Log in to reply
To get a while number yes but the problem wants a remander.
Much as I understand the solution, in my world, [97] is a 2 digit number not a 3 digit number. The correct response should be [097] surely to meet the original premise!
Log in to reply
97 is the remainder, which is what we are asked to find. It is not the three digit number by which we devide 31513 and 34369.
408 is also a 3 digit factor of 2856
(Method without using a calculator.)
If 3 1 5 1 3 ≡ 3 4 3 6 9 mod n , then n must be a divisor of their difference, which is 2 8 5 6 . It is easy to see that this goes about 11 times in the first given number and 12 times into the second given number; indeed, 3 1 5 1 3 − 1 1 ⋅ 2 8 5 6 = 9 7 ; 3 4 3 6 9 − 1 2 ⋅ 2 8 5 6 = 9 7 . Therefore the remainder after division by n will be 9 7 mod n ; because n > 9 7 , the remainder will be exactly 9 7 .
Great solution! I was too focused on finding a 3 digit number, so I went and got the factors of 2856, I never thought of using 2856 itself.
97 is not a three digit number
Log in to reply
The divisor has to be a three-digit number; the remainder doesn't have to be.
Hi Arjen, is there any more workings you could give? I have a very long way with a spreadsheet of all possible factors as I figured that threedigitfactor x (factor34369 - factor31513)=2856 and selected only the threedigitfactors={102,119,136,168,204,238,408,476,714,952} and ran the mod on the large and larger number divided by the factor. Where that set interacted with a common remainder of 97 I was surprised this occurred at more than one factor, the subset {102,119,136,168,204,238}. They are all even and the remainder 97 is prime
Others have written about the nice property of modulo (subtract the numbers and the remainder must be a divisor of the difference). But for the curious, those 3 digit numbers are 102,119,136,168,204,238,357,408,476,714 and 952.
I first came up with 102. It's wrong because? Thanks
Log in to reply
102 is one the three-digits number that is a divisor of both 31513 and 34369 but is not the remainder (if you divide by 102 you get a reminder of 97)
34369 - 31513 = 2856
Factorising we get 3 digit no. as .... 714 , 357 , 119. All are multiple or sub-multipleof each other. Remainder for 31513 / 714 = 97
Background logic :
Let x be the three digit number. Let
mx + r = 31513 .............. (1)
And nx + r = 34369 ........ (2)
Where m , n , r >=0 & m , n , r € Z+
Subtracting (2) from (1) : x * (n-m) = K (say) Here K = 2856 = 2 x 2 x 2 x 3 x 119
There may be many such x-s with three digits that make K as a factor of it.. they all are multiples or submultiples of that particular x.
And all such numbers will hv same remainder r, with both given numbers.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
|
1 2 3 4 5 6 7 8 9 10 11 12 |
|
Amazing! I am learning/want to be good at coding. But I can "read" this perfectly!
I might use what you did to practice problem solving with coding!
I didn't use any fancy mathematics here. We know that r + xd = 31513 and r + yd = 34369. Subtracting the first equation from the second gives (y-x) d = 2856. (This is where the people using modulo arithmetic get 2856 from.)
2856 factors into 2^3 * 7 * 51, and we know d divides that. The possible divisors are therefore 357 (7 * 51), 408 (8 * 51) and 714 (2 * 7 * 51). Any of those .divisors yields 97 as the remainder. Not as elegant a solution as some, but also not dependent on any mathematical knowledge beyond algebra.
The difference of the numbers 34369 and 31513 must be divisible by the three digit number. The difference is 2856. So we get 2856=(the three digit number )*(an integer). The prime factorization of 2856 is 3X8X7X17.. As we know that 31513 and 34369 are not divisible by 3 and 8. So the three digit number must be 7X17 which is 119. The remainder is therefore 31513 mod 119=97.
34369 mod x= 31513 Subtract 31513 from the left side to yield 2856 mod x=0. All of the three digit factors of 2856 will result in the same remainder, which is 97.
31513=r(mod a)
34369=r(mod a)
Subtracting,
2855=0(mod a)
Therefore,
2855*11=0(mod a)
31416=0(mod a)
Therefore,
34369=97(mod a)
There are 11 numbers that fulfill this condition, they are 102, 119, 136, 168, 204, 238, 357, 408, 476, 714, 952. Interestingly remainder in all cases is 97.
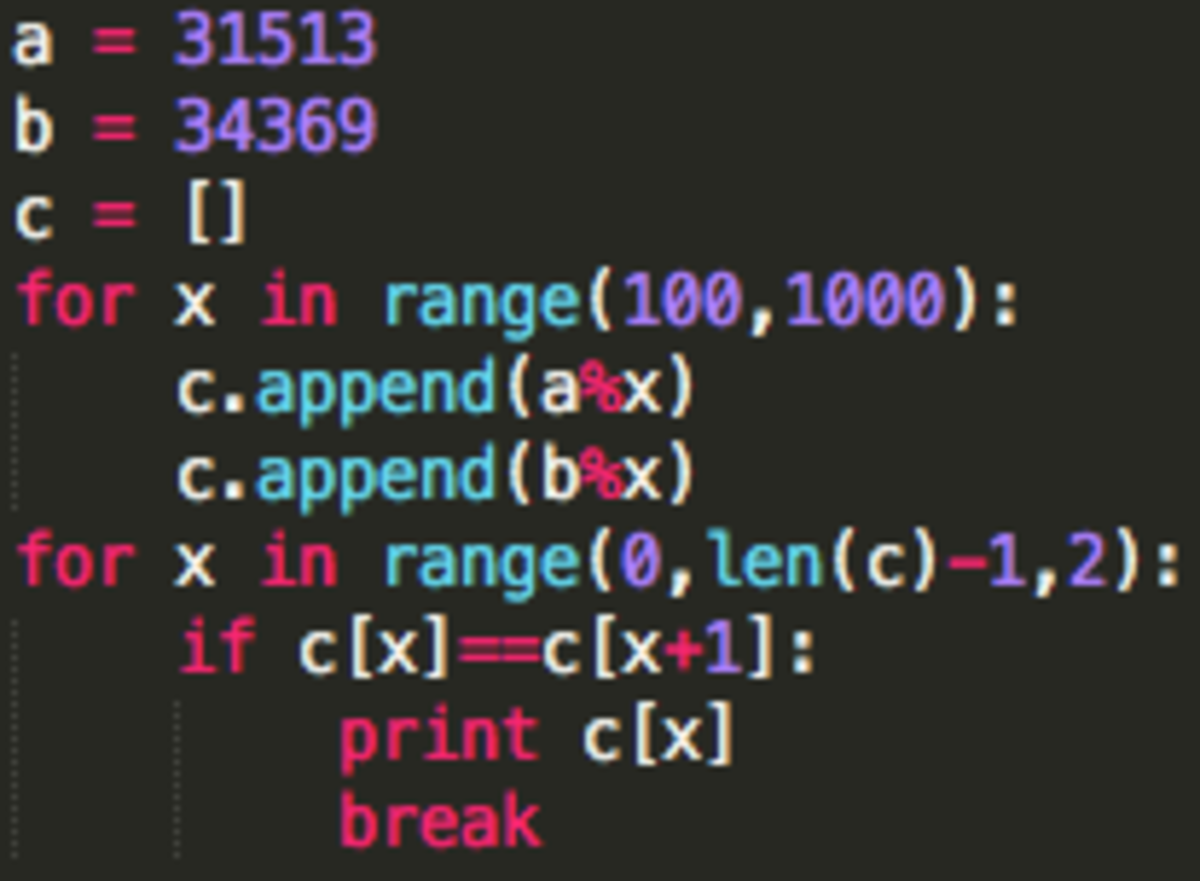
It is possible to write a simple program in order to solve this problem in python:
for i in range(100,1000):
rem1=31513%i
rem2=34369%i
if rem1 == rem2:
print(rem1)
break
I wrote a code in C# to solve this problem :
for(int i=100 ; i<=999; i++){
if(31513%i == 34369%i ){
the_answer=31513%i ;
breack;
} }
I have found the number using a graph:
-
define x n = mod(34369,n) and y n = mod(31513,n)
-
define z n = x n - y n
Then run a cycle for n =100 until n =999 to generate a matrix of z n . Plot all z n on y-axis and n on x-axis. Every n that gives z n = 0 is a 3-digit number divided by which the reminders of 34369 and 31515 are equal. Pick one of the numbers (zoom in), for example 102, to get mod(34369,102)=97 and mod(31513,102)= 9 7 .
Here is the plot with y-axis limits set to (-1,1):
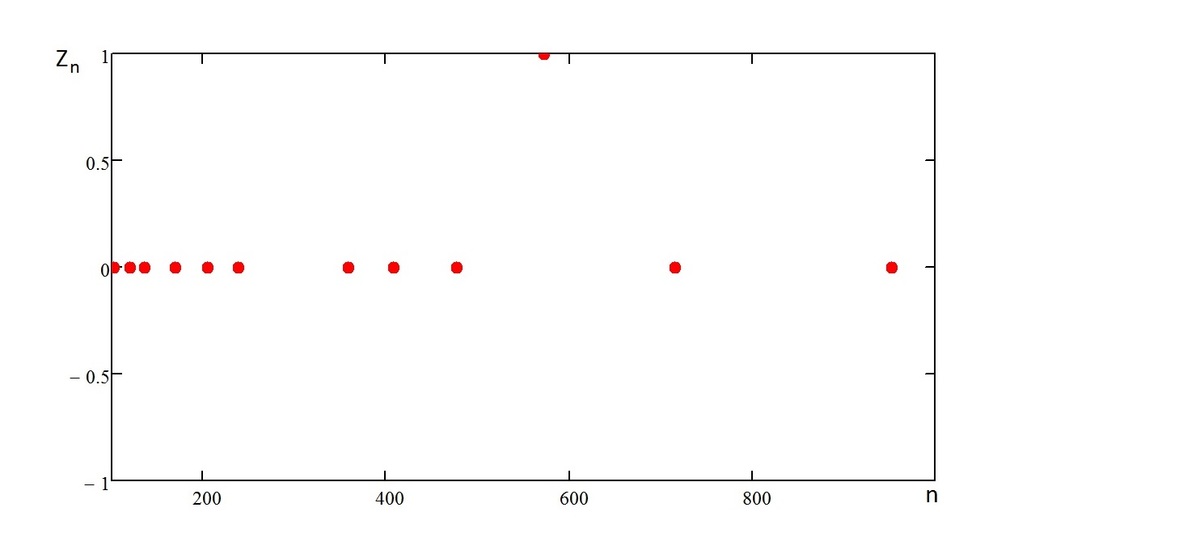
This is more like a hack
Question reformatted as a modular equavaluence is 3 1 5 1 3 ≡ 3 4 3 6 9 ( mod n ) . Substract left side from the eqaution for: 2 8 5 6 ≡ 0 ( mod n ) , which means that n can be 2 8 5 6 as x ≡ 0 ( mod x ) . Since we are looking for a 3-digit number, we can use 7 1 4 because 2 8 5 6 = 7 1 4 ⋅ 4 and if two numbers are congruent modulo x ⋅ y , they will be congruent modulo x . The remainder of the division 3 1 5 1 3 ÷ 7 1 4 is 9 7 .
The difference of the two numbers must be divisible by that three digit number, since the remainders have eliminated.
3 4 3 6 9 − 3 1 5 1 3 = 2 8 5 6
Three digit factors of 2856 include 168, 357, 714... all of them yields the same remainder when dividing 34369 which is 9 7