Different SHM

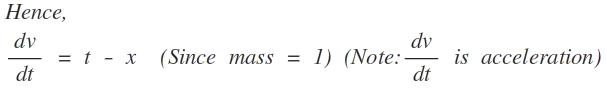
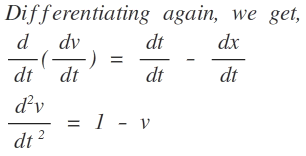
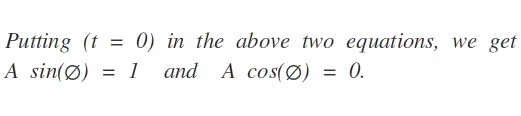
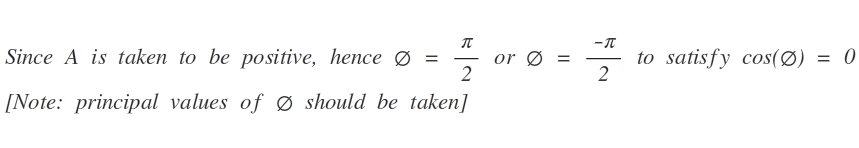
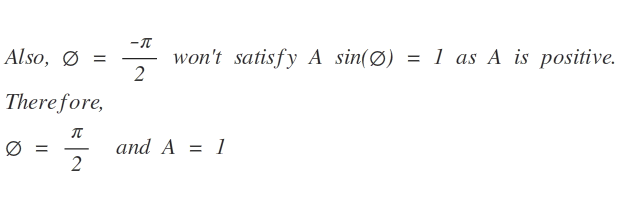
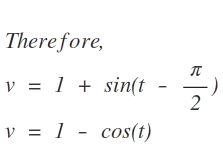
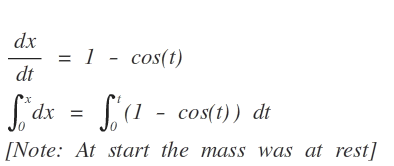
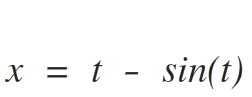
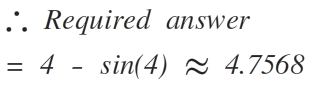
This is another method if you do not know how to solve differential equations-

Given ,

$a = t-x$

Differentiating w.r.t $t$

$\dfrac{da}{dt} = 1-v$

$\dfrac{dv}{dv}\times \dfrac{da}{dt} = 1-v$

$\left(\dfrac{dv}{dt} \right) \times da = dv - vdv$

$\displaystyle \int \limits_{0}^{a} ada = \int \limits_{0}^{v} dv - \int \limits_{0}^{v} vdv$

$a^2 = 2v - v^2$

$\dfrac{dv}{dt} =\displaystyle \sqrt{2v-v^2}$

$\displaystyle \int \limits_{0}^{v} \dfrac{dv}{\sqrt{2v-v^2}} = \int \limits_{0}^{t} dt$

$v-1 = - \sin{\left(\dfrac{\pi}{2} - t \right)}$

$v-1 = -\cos {t}$

$\displaystyle \int \limits_{0}^{x} dx = -\int \limits_{0}^{t} \cos{t} + \int \limits_{0}^{t} dt$

$x = t -\sin{t}$

Putting $t =4$

$\boxed{x = 4.7568}$

Can't we directly think it as SHM who's mean position has velocity 1m/s and particle will start from negative side so x = t - sin( t )