Different Voltage for the Same Power
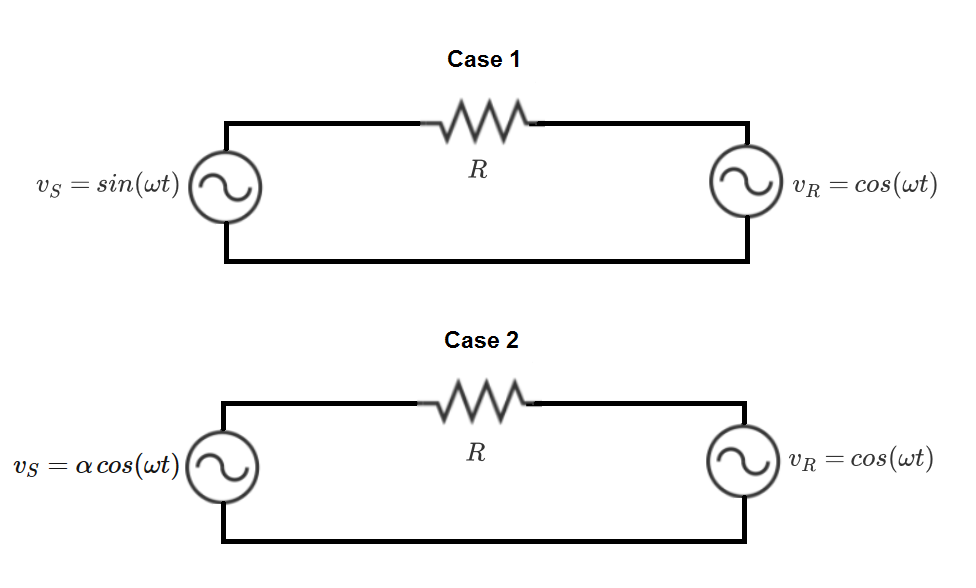
If the resistor dissipates the same average power (over an integer number of cycles) in both cases, what is the value of ?
Details and Assumptions:
- The two circuits (cases 1 and 2) have the same resistance and operate at the same frequency
-
is a positive number
The answer is 2.4142.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The key to solving this one is to think of the sinusoids as complex numbers. Note that in the first case, v S and v R have the same magnitude, and v S lags v R by 90 degrees. Find the voltage difference in case 1:
Case 1:
Δ v = v S − v R = 1 ∠ − 9 0 ∘ − 1 ∠ 0 ∘ = 2 ∠ − 1 3 5 ∘
In case 2, the two sinusoids have the same phase, so the voltage difference is more straightforward.
Case 2:
Δ v = v S − v R = α ∠ 0 ∘ − 1 ∠ 0 ∘ = ( α − 1 ) ∠ 0 ∘
In order for the same average power to be dissipated in both cases, the magnitudes of the voltage differences must be the same. Also, we know that α is a positive number:
α − 1 = 2 α = 1 + 2 ≈ 2 . 4 1 4 2