Different Ways Of Expressing The Same Thing
6 × 1 , 3 × 2 , 2 × 3 , 1 × 6
Andy just learned about multiplication in school. He found that there were 4 possible ways to express 6 as a product of 2 positive integers, as shown above.
If he wanted to write 6 as s product of 3 positive integers instead, what is the total number of ways to express it?
The answer is 9.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
6 = 2 × 3 .
Suppose that we have 3 numbers whose product is 6. Let them be represented by
(
a
,
b
,
c
)
.
We just need to answer "Which term is divisible by 2?" and "Which term is divisible by 3?"
There are 3 possibilities for which term is divisible by 2, and also 3 possibilities for which term is divisible by 3.
For example, if
c
is divisible by 2 and
b
is divisible by 3, then we have the solution
(
1
,
3
,
2
)
.
Hence, by the rule of product, there are 3 × 3 possible cases.
6 = 1 ⋅ 1 ⋅ 6 = 1 ⋅ 2 ⋅ 3 . The answer is just the sum of number of ways to permute them. 1 ⋅ 1 ⋅ 6 has 3 permutations while 1 ⋅ 2 ⋅ 3 has 6 permutations so the answer is 9.
6 can be written as the product of 1,2 and 3. These three distinct factors can be arranged in 3 ! = 6 ways.
6 can also be written as the product of 1,1 and 6. These can be arranged in 3 ways, (corresponding to the 6 being the first, second or third factor).
There are no other ways to express 6 as the product of three positive integers, and so our answer is
6 + 3 = 9
Let's break this down into a much simpler problem.
First of all, recognize the only new answers we can make involve multiplying the existing answers involving two integers by 1 .
Then we have two lists of three integers, that, when multiplied together have a product of 6 .
These lists are 6 , 1 , 1 and 3 , 2 , 1 . Let's substitute in letters for our numbers to give n , k , k and j , k , l . Now we can use one list or the other list to make a product equal to six, so we will calculate the number of permutations possible with each individual list, and then add the results by rule of sum.
Number of ways to permute n , k , k :
2 ! 3 ! = 3 .
Number of ways to permute j , l , k :
3 ! = 6 .
Thus our answer is 3 + 6 = 9 .
This is actually a fairly simple problem: arrange 4 items in as many ways as possible, while choosing 3 of them. It's kind of a mess, but here's my lovely representation: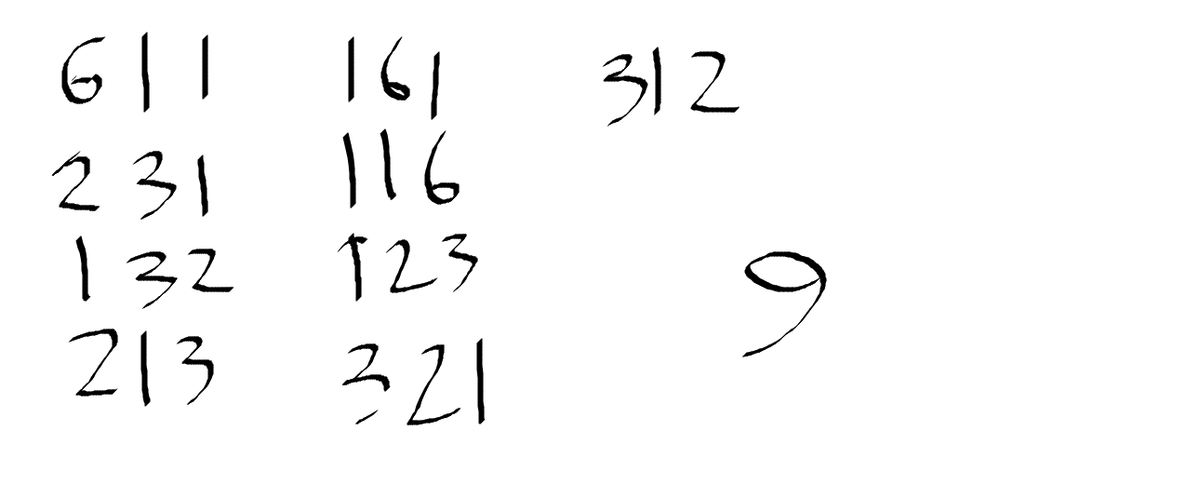 It was kind of a stream-of-consciousness bit, but my mental process was to write out the solutions with 6, 1, and 1, and then the solutions with 3, 2, and 1.
It was kind of a stream-of-consciousness bit, but my mental process was to write out the solutions with 6, 1, and 1, and then the solutions with 3, 2, and 1.
I should really be working on my biology packet, ha. This is more fun.