Length Of A Helix
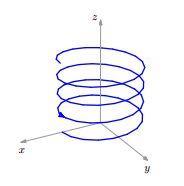 Consider the cylindrical helix in
R
3
whose equations are
Consider the cylindrical helix in
R
3
whose equations are
x = 3 cos ( t ) y = 3 sin ( t ) z = 4 t
What is the length of this helix from t = 0 to t = 4 0 3 ?
The answer is 2015.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Moderator note:
This "rolling out of the cylinder" is the standard trick for the competition problem about the length of a vine which grows by winding around a stick. It presents a simple geometric interpretation of this "3-d" length.
Even I have to admit that sometimes the solutions without calculus are the easiest and prettiest.
f(t) = (x(t),y(t),z(t)) = (3 cos(t), 3 sin(t), 4t); f ' (t) = (-3 sin(t), 3 cos(t), 4)
Lenght (helix) = ∫ 0 4 0 3 ∣ ∣ f ′ ( t ) ∣ ∣ d t = ∫ 0 4 0 3 9 s i n 2 ( t ) + 9 c o s 2 ( t ) + 1 6 d t = ∫ 0 4 0 3 2 5 d t = ∫ 0 4 0 3 5 d t = 5 ⋅ 4 0 3 = 2015
It is quite risky not to think in Calculus unless we have made a good mind set after a careful thought. If relation between x, y and z become more complicated, then a lack of caution could easily make a mistake. An opened-up triangle is a special case. Just be more careful, my advice to everyone.
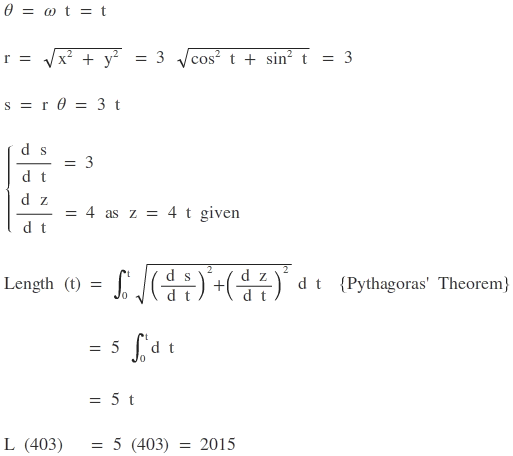
A solution without calculus: If you roll out the cylinder, the helix turns into a straight line that is the hypotenuse of a right triangle with horizontal side 3 ∗ 4 0 3 and vertical side 4 ∗ 4 0 3 . Thus the length of the helix is 5 ∗ 4 0 3 = 2 0 1 5