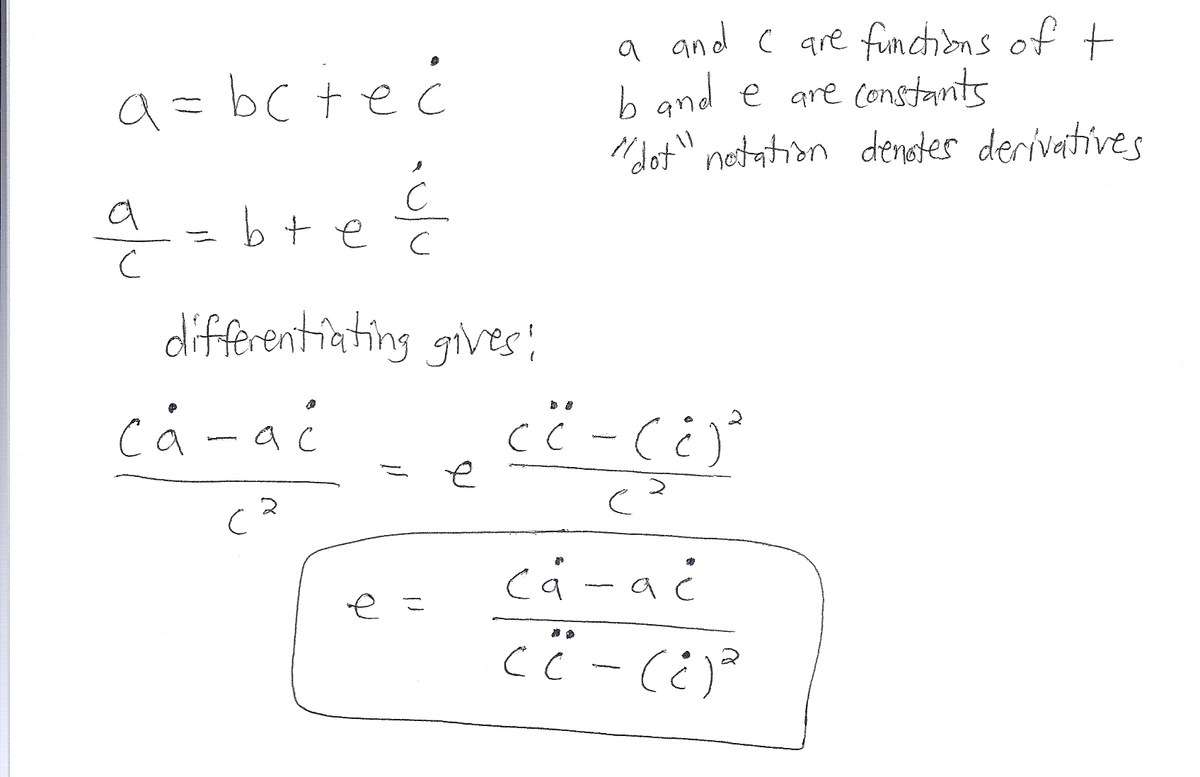Differentiate It Away

Suppose we have the following relationship:

$a(t) = b*c(t) + e*\frac{d}{dt} c(t)$

The " $*$ " above denotes multiplication. As shown above, $a(t)$ and $c(t)$ are functions of the parameter $t$ , and parameters $b$ and $e$ are constants. Suppose that we want to solve for $e$ without referring to $b$ . The parameter $e$ can be written as:

$\Large{e=\frac{c(t) * \frac{d^{W}}{dt^{W}} a(t) -a(t) * \frac{d^{X}}{dt^{X}} c(t) }{c(t) * \frac{d^{Y}}{dt^{Y}} c(t) -(\frac{d^{Z}}{dt^{Z}} c(t))^{2} }}$

Parameters $W, X, Y,$ and $Z$ denote the numbers of derivatives of their respective functions. Determine $(W+X+Y+Z$ ).