Dihedral Angle of an Icosidodecahedron
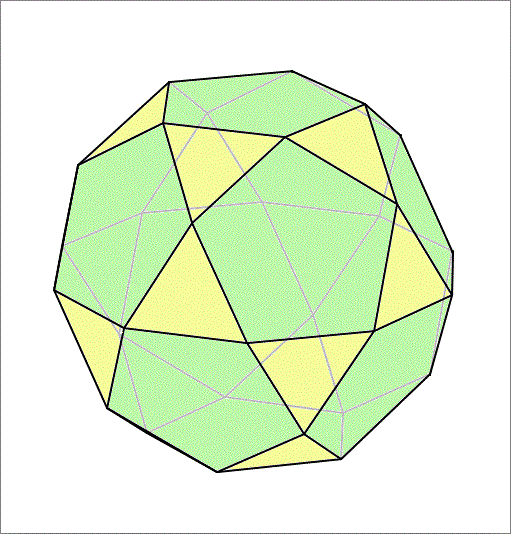
The so-called icosidodecahedron is depicted in the figure above. It is the solid that results from the intersection of a dodecahedron (green) and an icosahedron (yellow) of a specific relative scale. This is shown in the figure below. Its faces comprise regular pentagons and equilateral triangles. Find the dihedral angle (the inner angle between two faces of a polyhedron), between a pentagonal face and an equilateral triangular face, in degrees.
Note: The requested angle is obtuse.
The answer is 142.62.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
If you extend the faces of all the pentagons of the icosidodecahedron, it will form a dodecahedron where each vertex is centered above one of the equilateral triangles.
A pentagon in the icosidodecahedron can be formed by joining the midpoints of a pentagon in the dodecahedron. Since the icosidodecahedron pentagon has sides of 1 , the dodecahedron pentagon has sides of s = 2 ⋅ 2 1 sec 3 6 ° = 2 1 ( 5 − 1 ) .
Each of the "extra" 2 0 pyramids formed by the difference of the dodecahedron and icosidodecahedron have equilateral triangle bases with sides of 1 and lateral edges of l = 2 1 s = 4 1 ( 5 − 1 ) . The apothem of the equilateral triangle base is a = 2 3 1 , and the radius is r = 3 1 , so by the Pythagorean Theorem the height of the pyramid is h = l 2 − r 2 = ( 4 1 ( 5 − 1 ) ) 2 − ( 3 1 ) 2 = 6 1 ( 3 3 − 1 5 ) .
The dihedral angle between the base and lateral face of the pyramid is then θ 1 = tan − 1 a h = tan − 1 2 3 1 6 1 ( 3 3 − 1 5 ) = tan − 1 ( 3 − 5 ) . That means the dihedral angle between a pentagonal face and an equilateral triangular face of the icosidodecahedron is θ 2 = 1 8 0 ° − θ 1 = 1 8 0 ° − tan − 1 ( 3 − 5 ) ≈ 1 4 2 . 6 2 ° .