Dihedral angles.

If n is the number of sides of the base of the pyramid, then as n approaches infinity, the pyramid approaches the shape of a cone. A cone has smooth sides, and so the angle between the slant faces of the pyramid as it becomes more cone shaped approach 180 degrees. $\cos(180^{\circ})=-1$

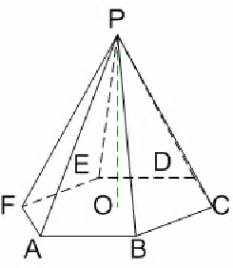
Assume the diagram above is any $n$ -gonal pyramid.

Let $OP$ be the height $H$ of the pyramid, $\theta = \dfrac{2\pi}{n}$ , and $r$ be the radius of the $n$ -gon.

Let $E: (-r\cos(\theta), r\sin(\theta), 0)$ , $A: (-r\cos(\theta), -r\sin(\theta), 0)$ , $F: (-r,0,0)$ , $P: (0,0,H)$ .

$\vec{FP} = r\vec{i} + 0\vec{j} + H\vec{k} , \:\ \vec{EP} = r\cos(\theta)\vec{i} - r\sin(\theta)\vec{j} + H\vec{k}, \:\ \vec{AP} = r\cos(\theta)\vec{i} + r\sin(\theta)\vec{j} + H\vec{k}$

$\vec{u} = \vec{FP} \times \vec{EP} = Hr\sin(\theta)\vec{i} + Hr(\cos(\theta) - 1)\vec{j} - r^2\sin(\theta)$

$\vec{v} = \vec{FP} \times \vec{AP} = -Hr\sin(\theta)\vec{i} + Hr(\cos(\theta) - 1)\vec{j} + r^2\sin(\theta)$

$\vec{u} \cdot \vec{v} = -r^2 H^2\sin^2(\theta) + r^2 H^2(\cos(\theta) - 1)^2 - r^4\sin^2(\theta)$

$|\vec{u}| = |\vec{v}| \implies |\vec{u}| * |\vec{v}| = |\vec{u}|^2 = r^2 H^2 \sin^2(\theta) + r^2 H^2 (\cos(\theta) - 1)^2 + r^4\sin^2(\theta)$

$\implies \cos(\lambda) =$ $\dfrac{H^2(\sin^2(\theta) + (\cos(\theta) - 1)^2) - r^2\sin^2(\theta)}{H^2(\sin^2(\theta) + (\cos(\theta) - 1)^2) + r^2\sin^2(\theta)}$ .

After doing some very tedious simplifying we obtain:

$\cos(\lambda) = -\dfrac{(2h^2 + r^2)\cos(\theta) + r^2}{2h^2 + r^2 + r^2\cos(\theta)}$

$$

Let $BC = x$ be a side of the $n - gon$ , $AC = AB= r$ , $AD = h^*$ , and $\angle{BAD} = \dfrac{\pi}{n}$ .

$\dfrac{x}{2} = r \sin(\dfrac{\pi}{n}) \implies r = \dfrac{x}{2 \sin(\dfrac{\pi}{n})} \implies h^* = \dfrac{x}{2} \cot(\dfrac{\pi}{n}) \implies A_{\triangle{ABC}} = \dfrac{1}{4} \cot(\dfrac{\pi}{n}) x^2 \implies$

$A_{n - gon} = \dfrac{n}{4} \cot(\dfrac{\pi}{n}) x^2 \implies V_{p} = \dfrac{n}{12} \cot(\dfrac{\pi}{n}) x^2 H$

The volume of the sphere $V_{s} = \dfrac{4}{3} \pi R^3$

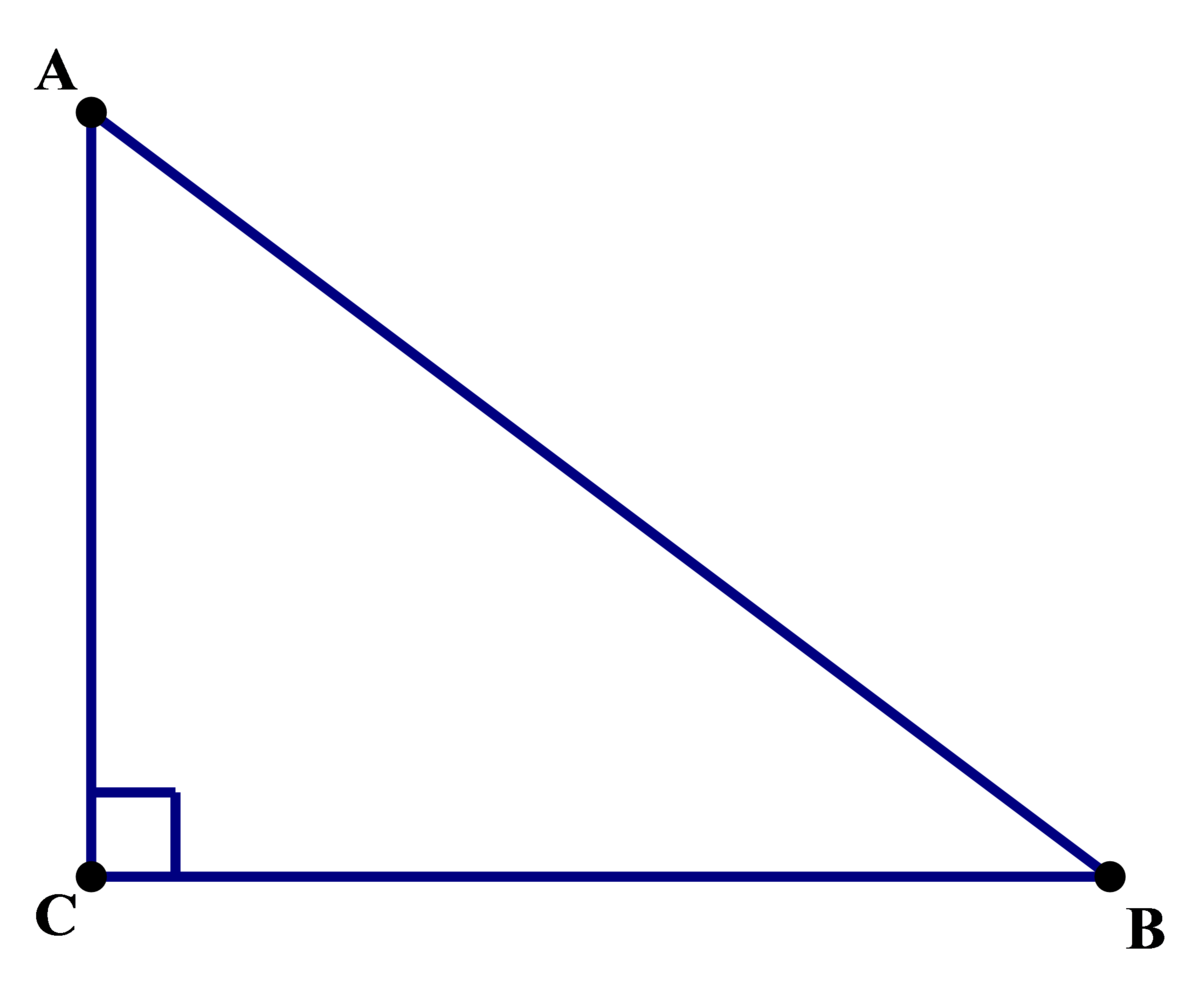
Let $H$ be the height of the given pyramid.

In the right triangle above: $AC = H - R, BC = \dfrac{x}{2 \sin(\dfrac{\pi}{n})}, AB = R \implies$

$R^2 = (H - R)^2 + \dfrac{x^2}{4} \csc^2(\dfrac{pi}{n}) \implies x^2 = 4H(2R - H) \sin^2(\dfrac{\pi}{n})$

$\implies V_{p}(H) = \dfrac{n}{6} \sin(\dfrac{2\pi}{n}) (2RH^2 - H^3) \implies$

$\dfrac{dV_{p}}{dH} = \dfrac{n}{6} \sin(\dfrac{2\pi}{n}) (H) (4R - 3H) = 0$ , $H \neq 0 \implies H = \dfrac{4R}{3} \implies x^2 = \dfrac{32}{9} \sin^2(\dfrac{\pi}{n}) R^2 \implies x = \dfrac{4 \sqrt{2}}{3} \sin(\dfrac{\pi}{n}) R$

$H = \dfrac{4R}{3}$ maximizes $V_{p}(H)$ since $\dfrac{d^2V_{p}}{dH^2}|_{(H = \dfrac{4R}{3})} =\dfrac{-2n}{3} \sin(\dfrac{\pi}{n}) R < 0$

$H = \dfrac{4R}{3}$ and $x^2 = \dfrac{32}{9} \sin^2(\dfrac{\pi}{n}) R^2$ .

From above $r = \dfrac{x}{2 \sin(\dfrac{\pi}{n})}$ $\implies r^2 =\dfrac{x^2}{4 \sin^2(\dfrac{\pi}{n})}.$

Using $\cos(\lambda) = -\dfrac{(2h^2 + r^2)\cos(\theta) + r^2}{2h^2 + r^2 + r^2\cos(\theta)}$ , where $\theta = \dfrac{2\pi}{n}$ and $H^2 = \dfrac{16 R^2}{9}$ and $x^2 = \dfrac{32}{9} \sin^2(\dfrac{\pi}{n}) R^2 \implies r^2 = \dfrac{8}{9} \implies$ $\cos(\lambda(n)) = -\dfrac{5\cos(\dfrac{2\pi}{n}) + 1}{5 + \cos(\dfrac{2\pi}{n})} \implies \lim_{n \rightarrow \infty} \cos(\lambda(n)) = \boxed{-1}.$