Dilated Steiner Inellipse
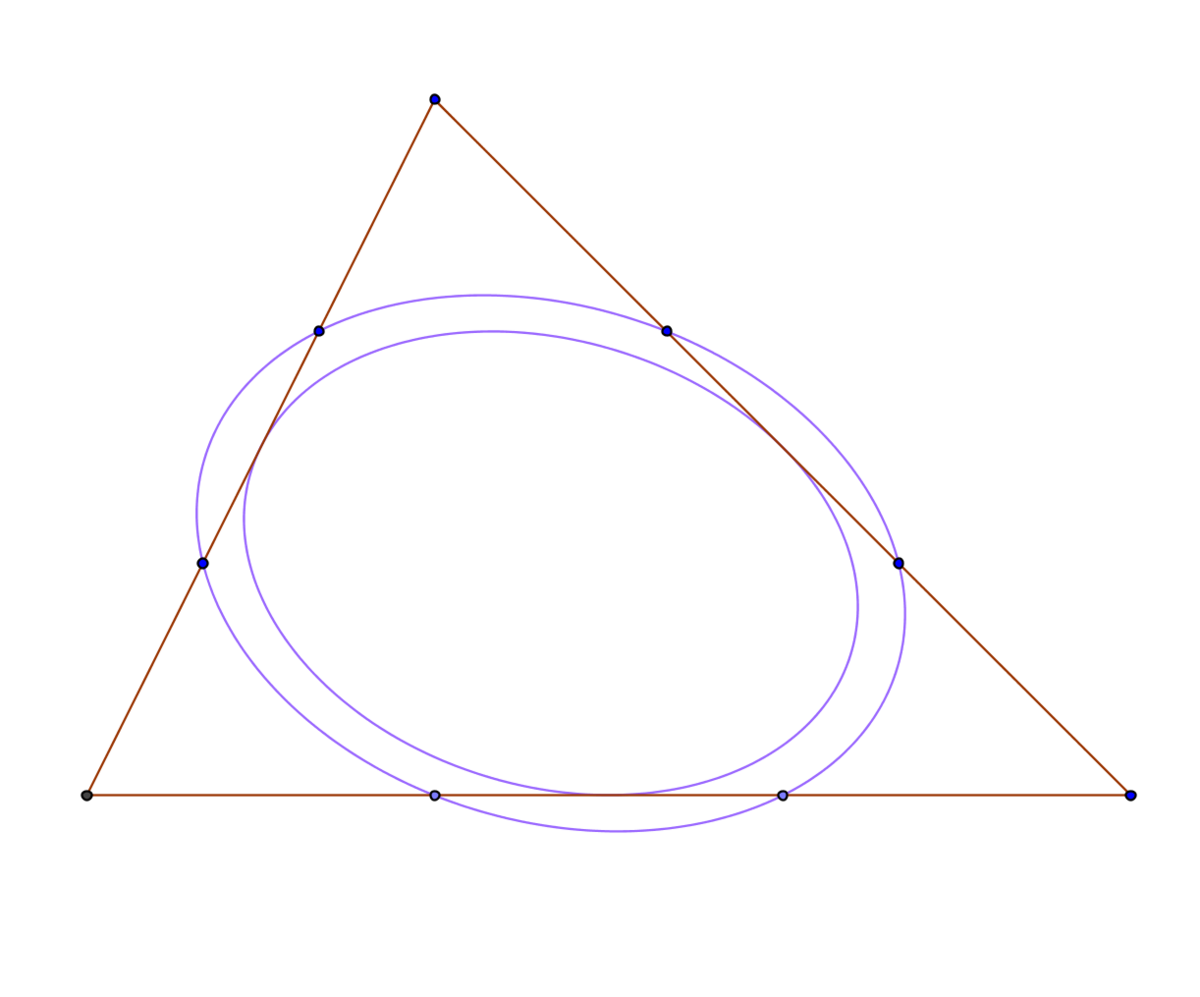
Triangle has vertices A = ( 0 , 0 ) , B = ( 9 , 0 ) , C = ( 3 , 6 ) . Its Steiner inellipse is dilated from triangle centroid. New ellipse trisects all three sides of the triangle A B C .
Given that the dilation factor can be expressed as b a , where a and b are positive integers with b square-free.
Find a + b .
The problem is original
The answer is 5.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Nice problem! I love problems that require very little computation when "done right".
May I steal this problem for the upcoming sixth edition of my text "Linear Algebra with Applications"? (with citation, of course)
Log in to reply
Reminder: Send me the amazon link when it's published.
Yes, you can use it.
Fine. Very simple.
Equation for big ellipse 4 x 2 + 2 x y + 7 y 2 − 3 6 x − 3 6 y + 7 2 = 0 and
a 2 = 1 1 − 1 3 7 2
b 2 = 1 1 + 1 3 7 2
c b 2 + b 2 = a 2
c b = 3 2 1 3
From https://brilliant.org/problems/complex-ellipse/?ref_id=1595309 find for little ellipse c l = 1 3
c l c b = 3 2
Answer 2 + 3 = 5 .
It is a factor of 3 2 . It is the same as a factor between trisecting circle and incircle radii for an equilateral triangle. It is independent of a triangle, in other words, Steiner inellipse dilated by a factor of 3 2 from centroid will trisect sides of any triangle.