Dilations and Reflections!
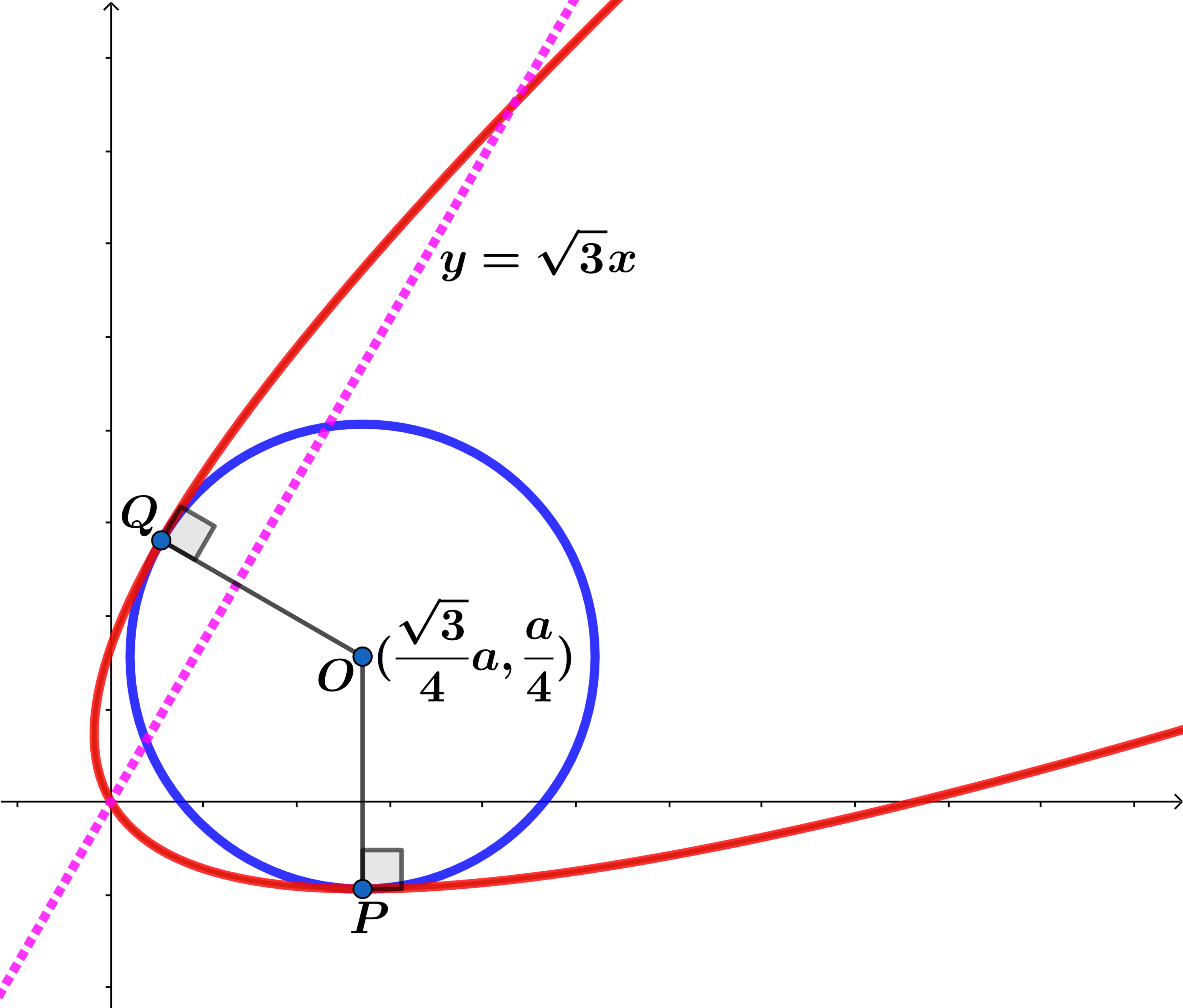
The parabola and a circle with radius with center , as shown above, is the image of a parabola and an inscribed circle which was reflected about the line then dilated by a factor of .
If the area of the region bounded by the above parabola and circle can be expressed as , where and are coprime positive integers, find .
The answer is 7.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Prior to doing the I will quickly derive the equations of a reflection of a point about some line.
The given line has slope m ⟹ m P P ′ = m ⊥ = − m 1 ⟹
m y + x = b m + a
and the given line is:
y − m x = − m x 0 + y 0
Solving the system we obtain:
x = m 2 + 1 m 2 x 0 + ( b − y 0 ) m + a = 2 a + a ′
y = m 2 + 1 b m 2 + ( a − x 0 ) m + y 0 = 2 b + b ′
Solving for a ′ and b ′ we obtain:
a ′ = m 2 + 1 2 m 2 x 0 + 2 ( b − y 0 ) m + ( 1 − m 2 ) a
b ′ = m 2 + 1 b m 2 + 2 ( a − x 0 ) m + 2 y 0 − b
m = tan ( θ ) ⟹
a ′ = ( a − x 0 ) cos ( 2 θ ) + ( b − y 0 ) sin ( 2 θ ) + x 0
and
b ′ = ( a − x 0 ) sin ( 2 θ ) − ( b − y 0 ) cos ( 2 θ ) + y 0
Replacing a , b , a ′ and b ′ by x , y , x ′ and y ′ respectively we obtain:
x ′ = ( x − x 0 ) cos ( 2 θ ) + ( y − y 0 ) sin ( 2 θ ) + x 0
y ′ = ( x − x 0 ) sin ( 2 θ ) − ( y − y 0 ) cos ( 2 θ ) + y 0
m = tan ( θ ) = 3 ⟹ θ = 3 π and since y = 3 x passes thru the origin, using the equations of reflection above with a dilation factor of 2 1 , we obtain:
x = 2 1 ( − 2 1 x ′ + 2 3 y ′ )
y = 2 1 ( 2 3 x ′ + 2 1 y ′ )
Using the above equations for the parabola x 2 − 2 3 x y + 3 y 2 − 3 x − y = 0 we obtain:
4 1 x ′ 2 − 2 3 x ′ y ′ + 4 3 y ′ 2
+ 2 3 x ′ 2 − 3 x ′ y ′ − 2 3 y ′ 2
+ 4 9 x ′ 2 + 2 3 3 x ′ y ′ + 4 3 y ′ 2
+ 3 x ′ − 3 y ′ − 3 x ′ − y ′ = 0
⟹ 4 x ′ 2 − 4 y ′ = 0 ⟹ y ′ = x ′ 2
and the center of the given circle ( 4 3 a , 4 a ) → ( 0 , a ) in the x ′ y ′ plane.
Using y ′ = x ′ 2 and center O ′ : ( 0 , a ) and P ′ : ( x ′ , y ′ ) = ( x ′ , x ′ 2 ) ⟹
D = r 2 = x ′ 2 + ( x ′ 2 − a ) 2 ⟹ d x d D = 2 x ′ ( 2 x ′ 2 + 1 − 2 a ) = 0
x ′ = 0 ⟹ x ′ = ± 2 2 a − 1 and the radius r = 1 ⟹ 4 a − 1 = 4 ⟹
a = 4 5 ⟹ x ′ = 2 3 ⟹ y ′ = 4 3 ⟹ the equation of the circle is
x ′ 2 + ( y ′ − 4 5 ) 2 = 1 and the portion of the circle needed is y ′ = 4 5 − 1 − x ′ 2 .
The area A = 2 ∫ 0 2 3 ( 4 5 − 1 − x ′ 2 − x ′ 2 ) d x
Letting x ′ = sin ( λ ) ⟹ d x ′ = cos ( λ ) d λ ⟹
A = 2 ( − 2 1 ∫ 0 3 π ( 1 + cos ( 2 λ ) ) d λ + ( 4 5 x ′ − 3 x ′ 3 ) ∣ 0 2 3 ) =
2 ( − 2 1 ( λ + 2 1 sin ( 2 λ ) ) ∣ 0 3 π + 2 3 )
= 4 3 3 − 3 π = b a a − a π ⟹ a + b = 7 .