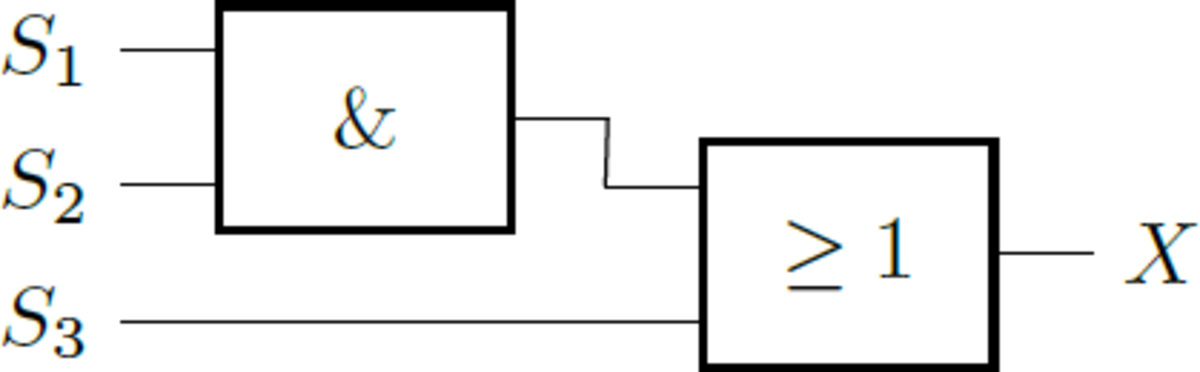Diode Logic

Electricity and Magnetism Level 4

Consider the following diode network with two resistors $R_1$ and $R_2$ , a light bulb, and three toggle switches S1, S2, and S3:

Which switch positions ensure that the light bulb is lit? Consider the circuit as a logical gate with the voltage $U = + U_0$ (high level) as TRUE and $U = 0$ (low level) as FALSE. The switches are the inputs of the logic gate, while the bulb serves as an output. Which logical expression represents the whole circuit?

In the answer options, we use the following abbreviations: $\begin{aligned} L &= \{\text{lamp is on}\} \\ S_n &= \{ \text{switch S}n\text{ is on} \}. \end{aligned}$

Assumptions: For the resistors, $R_2 \ll R_1$ applies so that in the off position of all switches, the electrical voltage drops practically only at the resistance $R_1$ , so that the output is at a low level and the lamp is not lit. Take the diodes as ideal rectifiers, which have no resistance in the forward direction and completely block the current flow in the reverse direction.

L = S_1 \text{ OR } S_2

L = S_1 \text{ AND } S_2 \text{ AND } S_3

L = S_1 \text{ OR } S_2 \text{ OR } S_3

L = (S_1 \text{ AND } S_2) \text{ OR } S_3

L = (S_1 \text{ OR } S_2) \text{ AND } S_3

L = S_3

1 solution

Markus Michelmann
Feb 4, 2018

We first consider the first diode pair. If one of the two switches S1 and S2 is in the off position, the corresponding diode is switched in the forward direction, so that a current flows through the resistor. Since the diode has no resistance in this position, the entire voltage drops at the resistor, so that the output is at zero potential. However, if both switches S1 and S2 are on, all nodes are at high level, so that also exists at the output of the potential $U = + U_0$ . The diode pair therefore acts as an AND gate with respect to the switches S1 and S2, so that the output has high level if and only if both switches are on.

The second pair of diodes is reversed poled, so that the current flows if one of the two inputs is at high level. In this case, the entire voltage drops again at the resistor, so that the output has the potential $U = + U_0$ . If both inputs are at low level ( $U = 0$ ), this applies also to the output. This circuit is thus an OR gate.

Thus, the entire circuit is represented by the expression

$L = (S_1 \text{ AND } S_2) \text{ OR } S_3$

I have to admit, the solution to this confuses me. I'm going to assume that what you are referring to as point "U" is directly above R2 (and therefore the voltage to the light "L").

The first part of your explanation makes sense, assigning an AND gate to the first 2 diodes. Then with S1 and S2 ON, the AND gate has a solution of TRUE. I understand that part. But, there is also the rest of the circuit to consider. Even with it being TRUE, I can't see how you will have +Uo at point U based on your assumptions. Specifically the reverse biased diodes (D1 and D2) will act as opens (infinite resistance) and are irrelevant in the parallel path between them and R1 so the effective resistance between Uo and the point just below R1 is the resistance of R1. I'll refer to this point as point M. Point M would be + with respect to point U and therefore diode D3 would be forward biased (resistance of 0 from the assumptions). This makes U=M. But does it also make U=Uo? Let's analyze...

With both S1 and S2 ON (and S3 still OFF), we basically have a circuit path consisting of +Uo -> R1 -> M -> D3 -> U -> R2/L -> ground. Correct me if I'm wrong, but with respect to point U this is a simple single loop circuit with 2 resistances, 1 before and 1 after. If R1=R2/L then U= half of +Uo. However, based on the assumptions with R2 << R1 , which would necessarily make R2/L significantly less resistance than R1, causing most of the voltage in this loop to drop across R1 and making point U significantly less than half of +Uo, which, while not 0, is much closer to being 0 than +Uo. I would consider that to be a FALSE solution at U.

With S3 on, though, we basically bypass all the above putting Uo directly on U so in this case U=Uo and the solution is TRUE.

Mike Serafin - 4 weeks ago

Diode Logic

1 solution

0 pending reports