Diophantine Equation
y 2 + 2 y = 7 x + 3
Find the number of ordered solutions ( x , y ) of the above equation, where x and y are both non-negative integers.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
Did the same way
Simpler argument using modular arithmetic.
The only possible factors of y+3 and y-1 are 1 and 7^n (n<x). This means y+3 must be congruent to 0 or 1 mod 7, and y-1 must be congruent to 0 or 1 mod 7. But y+3 = (y-1)+4, and if y-1 is congruent to 0 or1 mod 7, then y+3 must be congruent to 4 or 5 mod 7. y+3 cannot be congruent to both (0 or 1) and (4 or 5) mod 7, so no solution exists for non-negative integers.
The right side of the equation is certainly congruent to 1 mod 3. The left side of the equation is one less than a perfect square (We have y 2 + 2 y = ( y + 1 ) 2 − 1 ), so it can be written as n 2 − 1 = ( n − 1 ) ( n + 1 ) for some n ∈ N . That expression can only take the values 0 and -1 mod 3, so the equation can have no solutions in non-negative integers.
y
2
+
2
y
=
7
x
+
3
by adding 4 to both sides we get
y
2
+
2
y
+
4
=
7
x
+
7
(
y
+
2
)
2
=
7
x
+
7
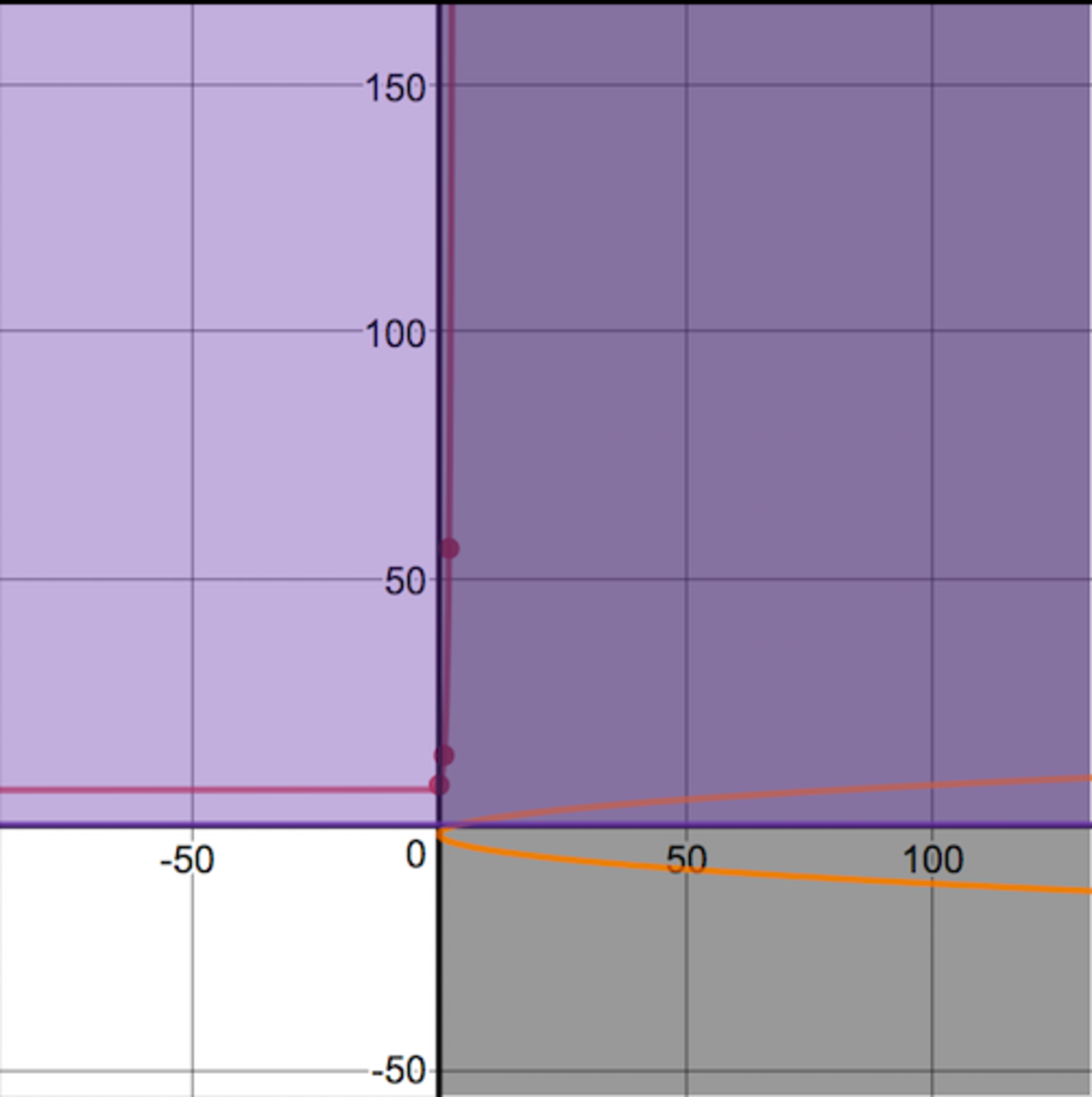
graphically
The
LHS
resembles has the graph of right arm of a parabola with
no vertex
and a starting point at
(4,0)
, where
y
is the input and
x
is the output. we observe that the graph keeps on stretching on the 1st Quad forever.
The
RHS
has the properties and the graph of an exponential function starting at the point
(0,8)
, with a horizontal asymptote at y=7 and as x approaches 7, y approaches limits.
we conclude that the two graphs will never intersect.
algebraically
since all
x
, and
y
values are non-negative integers, meaning {0,1,2,3,4,5,...)..it will be easier to make a system of two different equations where the output
Z
is the same.
1
(
y
+
2
)
2
=
Z
1
2
7
x
+
7
=
Z
2
in
1
all value inputs of
Y
result in outputs
Z
that are alternating between even and odd numbers consecutively : {(0,4),(1,9),(2,16),(3,25)...) in
2
whatever
x
input is, the output
Z_2
will always be even.
therefore
we can neglect all
Y
values that produce odd
Z1
s. those
Y
values are the odd integers only. now that we have restricted the
Y
inputs into being non-negative integers that are not odd numbers, we can
Simplify
. -
(
y
+
2
)
2
=
7
x
+
7
- RHS :
7
(
7
x
−
1
+
1
)
subtract 7/7 from both sides
-
7
(
y
+
2
)
2
−
7
)
=
7
x
−
1
LOG BOTH SIDES
- log
7
(
y
+
2
)
2
−
7
)
=
(
x
−
1
)
l
o
g
7
..log
7
(
y
+
2
)
2
−
7
)
=
x
l
o
g
7
−
l
o
g
7
- log
7
(
y
+
2
)
2
−
7
)
+
l
o
g
7
=
x
l
o
g
7
- log (
7
(
y
+
2
)
2
−
7
)
∗
7
)
=
x
l
o
g
7
divide by log 7
,then
perform log change of base
-
l
o
g
7
(
(
y
+
2
)
2
−
7
)
=
x
>>> for any allowed inputs of
Y
x will never be a positive integer
On rearranging the equation a bit, (y+1)^2=7^x+4. Now 7^x is odd therefore y+1 must be odd. Now we know odd squares are of form 8k+1. Reducing the rhs modulo 8 we get, (-1)^x +4 which can never be 1. Thus no solution.
Adding 1 to both sides we get ( y + 1 ) 2 = 7 x + 4 LHS is congruent to 0 or 1 mod 3 but RHS is congruent to 2 hence contradiction.
y 2 + 2 y = 7 x + 3 y 2 + 2 y − 3 = 7 x ( y + 3 ) ( y − 1 ) = 7 x
Now g c d ( y + 3 , y − 1 ) = g c d ( y − 1 , 4 ) .
So, g c d ( y + 3 , y − 1 ) will be 1 , 2 , 4
but in R.H.S. the whole number is a power of 7 .So here gcd will be form of 7 k where k is any integer.
So, only chance is if they are co-prime i.e. y − 1 = 1 ; y + 3 = 7 x which does not give any integral solution.
So, there is no integral solution exists.