Direction of reaction
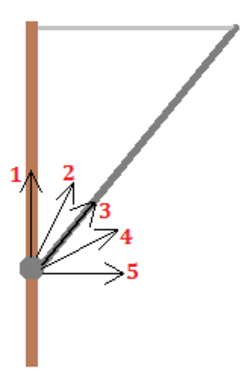 Homogenous rod is fixed at one point by a pivot about which it can rotate. In order to avoid rotation, upper end of the rod is suspended by a horizontal thread, which other end is anchored to the vertical wall. Think about statics and look at the drawn directions (1-5) of the force between the pivot and the rod.
Which number represents the right direction of the reaction force in pivot?
Homogenous rod is fixed at one point by a pivot about which it can rotate. In order to avoid rotation, upper end of the rod is suspended by a horizontal thread, which other end is anchored to the vertical wall. Think about statics and look at the drawn directions (1-5) of the force between the pivot and the rod.
Which number represents the right direction of the reaction force in pivot?
The answer is 2.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
We have 3 forces acting on the rod. The first is gravity force which acts in the center of the homogenous rod, the second is tension in the thread, and the third is reaction force of the pivot. Let us consider torques at the pivot. Since the rod rests, resulting torque is equal to zero, which yields m g × a / 2 = T × b (where ( a is length of the thread, and b is relative height of upper end of the rod to lower end). From that we get m g = 2 a b T . Reaction force at pivot has two components, horizontal and vertical. Horizontal is equal to T and vertical to m g . In our case T m g = 2 a b , so vertical component is more than a b times greater than horizontal , which means that direction is "upper" the direction 3, and however forms certain angle with vertical (so 1 is not the option). From that we get the final answer, that direction 2 is the right direction of the reaction force at the pivot.