Dirty Algebra
a 1 − a 2 = 6 1
Given that the equation above is fulfilled for 0 < a < 1 , find a 6 + ( 1 − a 2 ) 3 .
The answer is 0.5.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
sin 6 ( x ) + cos 6 ( x ) = ( sin 2 ( x ) ) 3 + ( cos 2 ( x ) ) 3 = ( sin 2 ( x ) + cos 2 ( x ) ) ( ( sin 2 ( x ) ) 2 + ( cos 2 ( x ) ) 2 − sin 2 ( x ) cos 2 ( x ) ) = 1 ( ( ( sin 2 ( x ) ) 2 + ( cos 2 ( x ) ) 2 + 2 sin 2 ( x ) cos 2 ( x ) − 3 sin 2 ( x ) cos 2 ( x ) ) ) = ( ( ( sin 2 ( x ) + cos 2 ( x ) ) 2 − 3 sin 2 ( x ) cos 2 ( x ) ) ) = 1 − 3 sin 2 ( x ) cos 2 ( x ) = 1 − 4 3 ⋅ 4 sin 2 ( x ) cos 2 ( x ) = 1 − 4 3 ( 2 sin ( x ) cos ( x ) ) 2 = 1 − 4 3 sin 2 ( 2 x )
Squaring the given equation gives ( a 1 − a 2 ) 2 = ( 6 1 ) 2 a 2 − a 4 = 6 1
Going back to the question, let's factor \[\begin{array}{} a^{6} + (1- a^{2})^{3} & = (a^{2})^{3} + (1- a^{2})^{3} \\& = (a^{2} + 1 - a^{2})((a^{2})^{2} - a^{2}(1 - a^{2}) + (1 - a^{2})^{2}) \\& = (a^{2} +1 - a^{2})(a^{4} - a^{2} +a^{4} +1 - 2a^{2} + a^{4}) \\& = (1)(3a^{4} - 3a^{2} + 1) \\& = (1)(3(-\frac{1}{6}) + 1) \qquad \left[ \because a^{2} - a^{4} = \frac{1}{6} \right] \\& = \boxed {\frac{1}{2} \rightarrow 0.5} \end{array}\]
Here is a proof without trigonometry:
a 1 − a 2 = 6 1 a 2 ( 1 − a 2 ) = 6 1 a 2 − a 4 = 6 1 0 = a 4 − a 2 + 6 1
Now let a 6 + ( 1 − a 2 ) 3 = S ,
a 6 − a 6 + 3 a 4 − 3 a 2 + 1 = S 3 a 4 − 3 a 2 + 1 = S a 4 − a 2 + 3 1 = 3 S
and subtract the first equation from the second one:
a 4 − a 2 + 3 1 − a 4 + a 2 − 6 1 = 3 S − 0 6 1 = 3 S S = 2 1
Take a = sin θ
sin θ cos θ = 6 1
sin θ × cos θ = 6 1
sin 6 θ + cos 6 θ = ( sin 2 θ + cos 2 θ ) ( sin 4 θ − sin 2 θ cos 2 θ + cos 4 θ )
= ( 1 ) ( ( sin 2 θ + cos 2 θ ) 2 − 2 sin 2 θ cos 2 θ − sin 2 θ cos 2 θ ) = 1 − 3 sin 2 θ cos 2 θ
⇒ a 6 + ( 1 − a 2 ) 3 = ( 1 ) ( 1 − 3 × 6 1 ) = 0 . 5
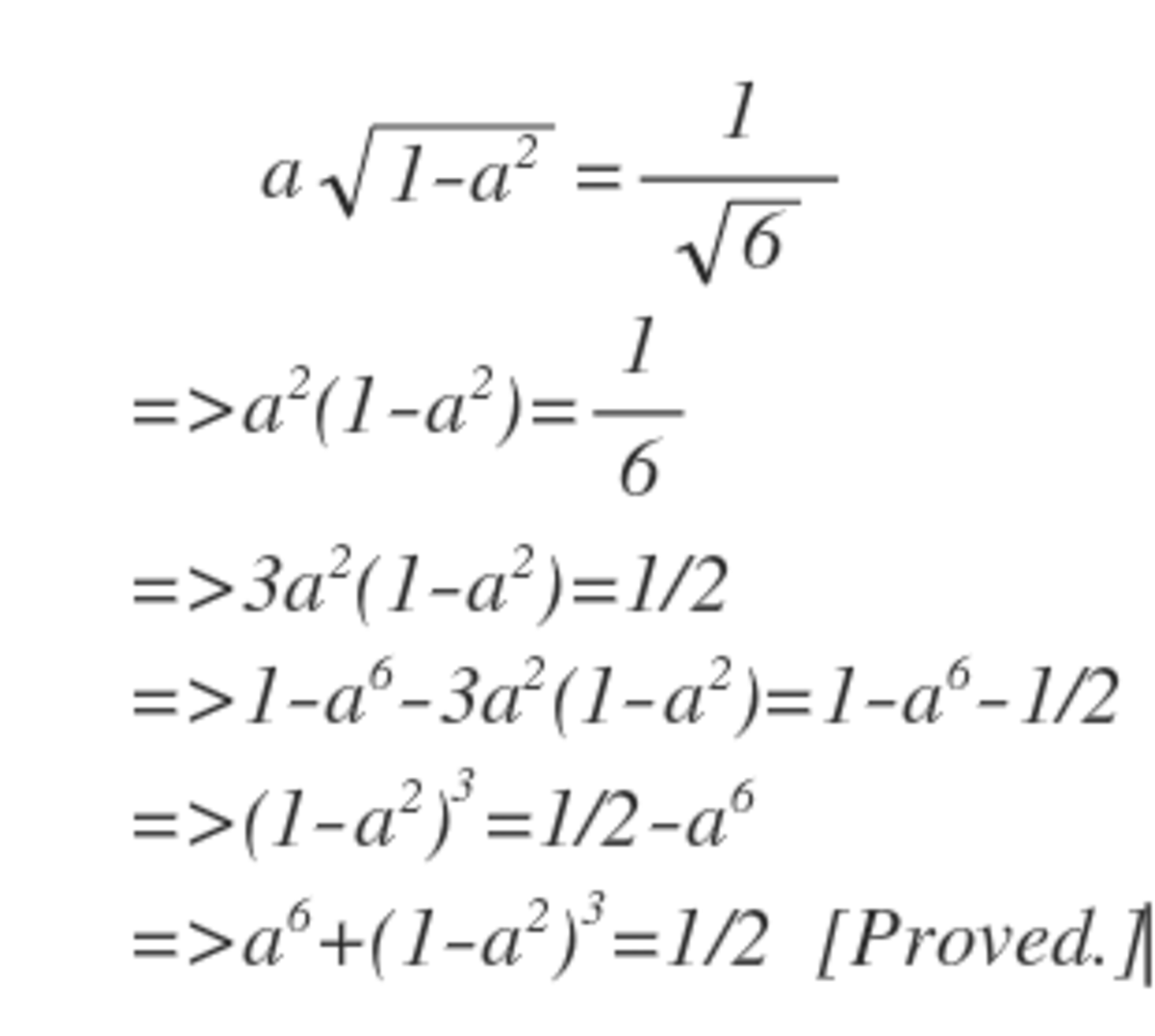
Let a = sin ( x ) , so 1 − a 2 = cos ( x )
Now we have sin ( x ) cos ( x ) = 6 1
Doubling both sides 2 sin ( x ) cos ( x ) = 6 2
or sin ( 2 x ) = 6 2
Now we need to find a 6 + ( 1 − a 2 ) 3
Which is equal to a 6 + ( 1 − a 2 ) 6
or
sin 6 ( x ) + cos 6 ( x )
Which is equal to (proof in comments section) 1 − 4 3 sin 2 ( x )
Which gives 1 − 4 3 ( 6 2 ) 2
= 2 1
Although this looks quite long, by this method, it can be done mentally in seconds.
Please upvote if you liked the solution.