Disappearing Triangles
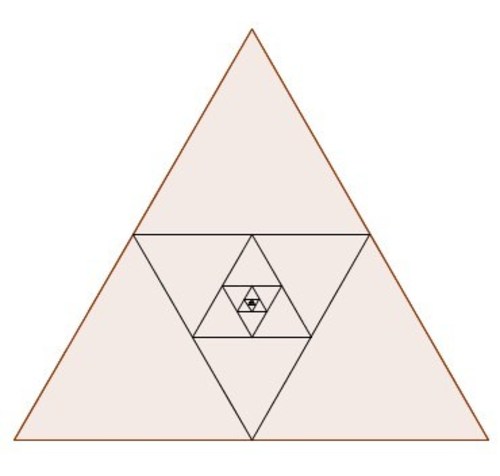 One side of an equilateral triangle is
cm. The midpoints of its sides are joined to form another triangle whose midpoints, in turn, are joined to form still another triangle. This process continues indefinitely.
One side of an equilateral triangle is
cm. The midpoints of its sides are joined to form another triangle whose midpoints, in turn, are joined to form still another triangle. This process continues indefinitely.
Find the sum of the perimeters of all these triangles that are defined above.
The answer is 192.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The perimeter of the largest triangle is 9 6 cm. The perimeter of the second triangle is only half that of the first because all the triangles are equilateral and they are being separated at the midpoints.
Thus the answer is 9 6 + 4 9 + 2 4 . . . .
This is an infinite geometric series. where the infinite sum is S ∞ = 1 − r t 1
This is then S ∞ = 1 − ( 2 1 ) 9 6 = . 5 9 6 = 9 6 × 2 = 1 9 2
since r = 2 1 and t 1 = 9 2