Disc rotating in a horizontal plane
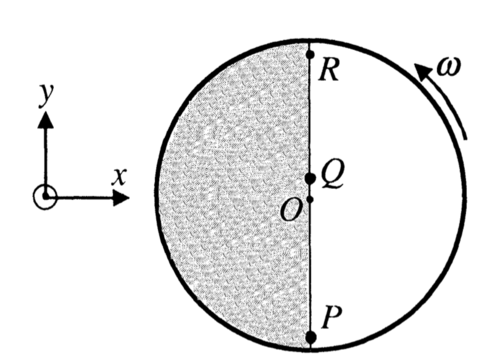 Consider a disc rotating in the horizontal plane with a constant angular speed
about its centre
. The disc has a shaded region on one side of the diameter and an unshaded region on the other side as shown in the figure. When the disc is in the orientation as shown, two pebbles
and
are simultaneously projected at an angle towards
. The velocity of projection is in the
plane and is same for both pebbles with respect to the disc. Assume that (i) they
land back on the disc before the disc has completed
rotation, (ii) their range is less than half the disc radius, and (iii)
remains constant throughout. Then
Consider a disc rotating in the horizontal plane with a constant angular speed
about its centre
. The disc has a shaded region on one side of the diameter and an unshaded region on the other side as shown in the figure. When the disc is in the orientation as shown, two pebbles
and
are simultaneously projected at an angle towards
. The velocity of projection is in the
plane and is same for both pebbles with respect to the disc. Assume that (i) they
land back on the disc before the disc has completed
rotation, (ii) their range is less than half the disc radius, and (iii)
remains constant throughout. Then
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
0 solutions
No explanations have been posted yet. Check back later!