Discover the Height!

Geometry Level 3

In the image below, all the circles have the same diameter, the central circle is tangent to all other circles, and the other circles are tangent to the rectangle $ABCD$ (in 2 points), to the central circle and to the circle that is its borderer. Is given that $AB = 6 \ cm$ .

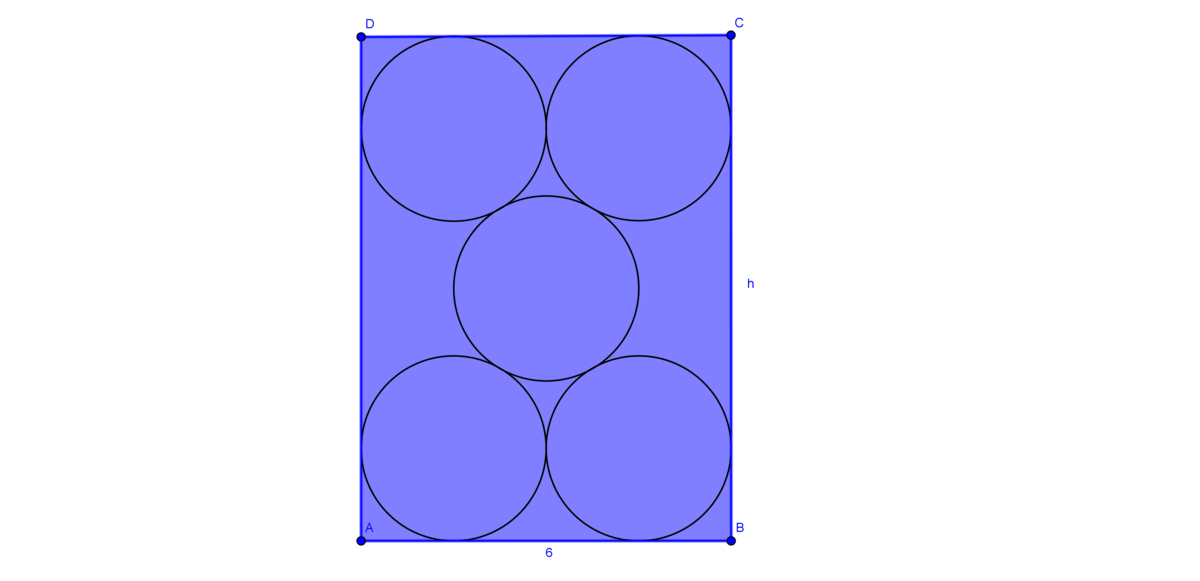
Determine the value of $BC$ in $cm$ .

{6\sqrt{3}} + {3}

{3} + {\sqrt{35}}

{3\sqrt{3}} + {3}

It's impossible to determinate! 9

1 solution

A Former Brilliant Member
Jul 14, 2017

If all of the circles have the same diameter, we can get that the diameter is $3 cm$ and the radius is $1.5 cm$ , because we have two equal diameters that together are $6 cm$ .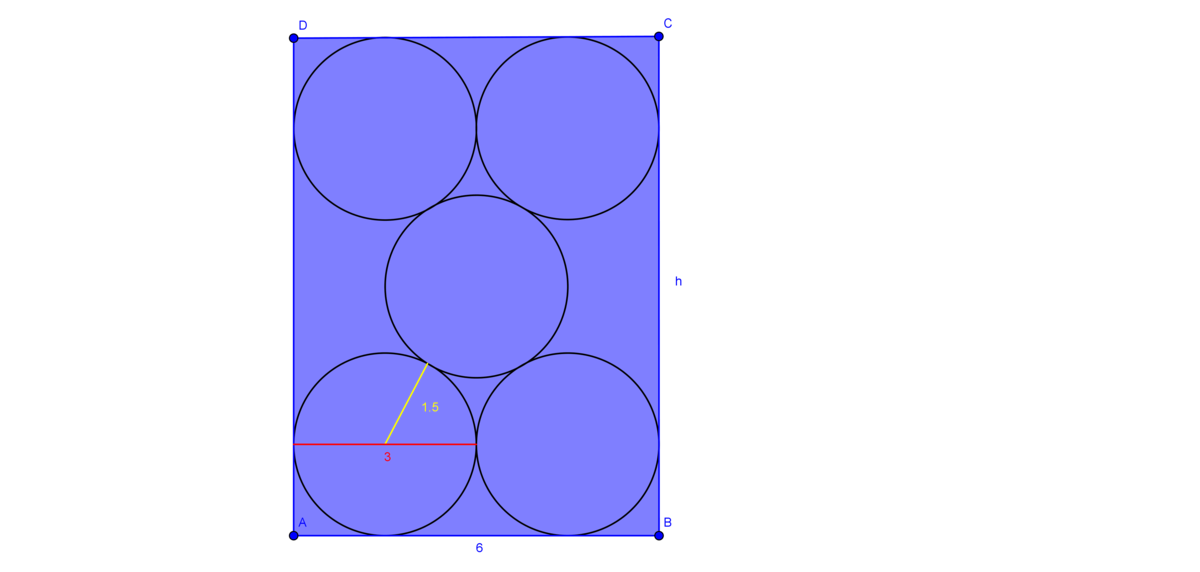

There are two equilateral triangles in the figure, that have $3cm$ size, as you can see here: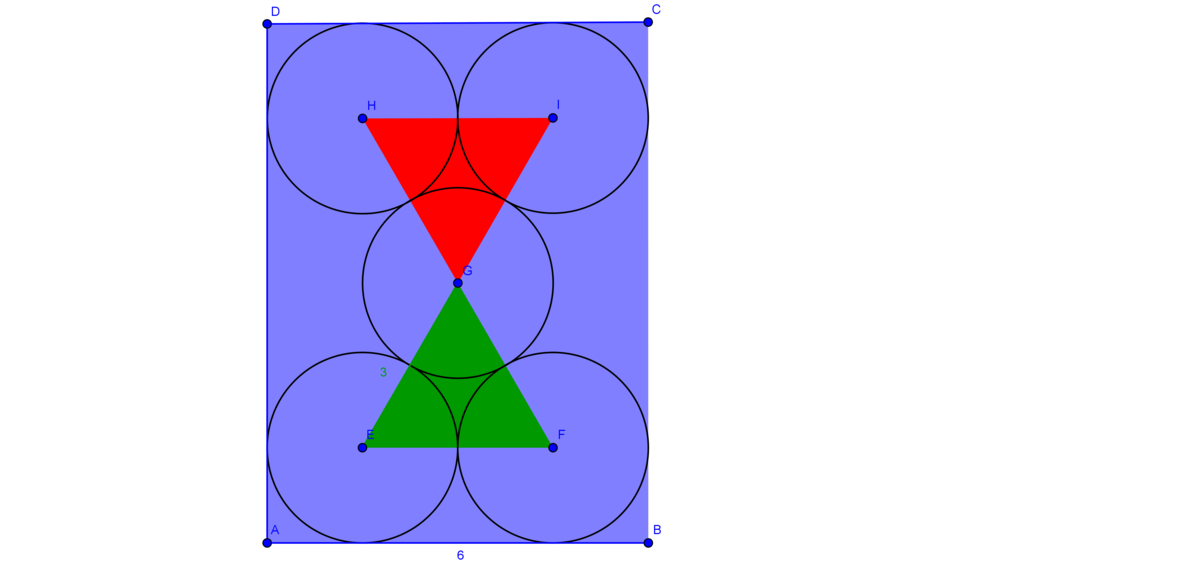

To get the height of the triangles, we will use the formula: ${h} = {{{l} \over {2}} \times \sqrt{3}}$ , so the height is ${3}\sqrt{3} \over {2}$ . But we need two times the radius of the circle to complete $BC$ .

${BC} = {2} \times {{{3}\sqrt{3} \over {2}}} + {{2} \times {1.5}}$

${BC} = {{3\sqrt{3}} + {3}} cm$

Discover the Height!

1 solution

0 pending reports