Discrete Differentiator Error

Consider a time sinusoid $x$ whose time derivative is $y$ .

$x(t) = \sin(\omega \, t) \\ y(t) = \omega \, \cos(\omega \, t)$

The derivative is larger by a factor $\omega$ and leads by 90 degrees. The ideal differentiator "transfer function" can therefore be expressed in the complex plane as:

$\vec{H} = j \, \omega \\ j = \sqrt{-1}$

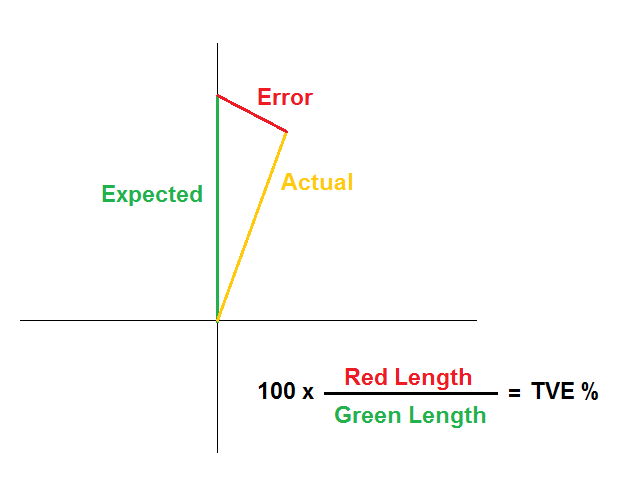
Considered in a context of polar coordinates, the magnitude of $\vec{H}$ is the differentiator gain, and the angle is the phase response (with the $j$ indicating a $+90^\circ$ shift - see the green line in the above graphic).

Suppose we generate a discrete sine wave by creating waveform samples separated by a time interval $T$ ( $k$ is an integer).

$x(k) = \sin(\omega \, k \, T)$

Then we generate a discrete derivative $y(k)$ as follows, using a difference quotient:

$y(k) = \frac{x(k) - x(k-1)}{T}$

This operation has an associated transfer function $\vec{H_d}$ , which is slightly different from the ideal transfer function $\vec{H}$ . In general, there may be deviations both in the gain and in the phase response. We would like to incorporate both types of error into a single metric, known as "total vector error" (TVE). Define the percentage TVE as follows:

$TVE \, \% = 100 \times \frac{|\vec{H_d} - \vec{H}|}{|\vec{H}|}$

This is effectively the length of the "error vector" divided by the length of the ideal transfer function vector (see graphic).

If ( $\omega = 120 \, \pi \, \text{rad/sec}$ ) and ( $T = \frac{1}{8000} \, \text{sec}$ ), what is the total vector error percentage $(\text{TVE} \%)$ for the discrete differentiator?

Note: For reference, a solution to a similar problem can be found here