Discs in Triangle
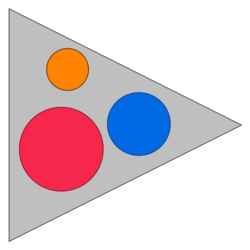
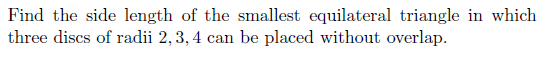
Find the side length (to 2 decimal places):
The answer is 19.052558883257.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
OMG!!!!!! I took this approach but made a mistake, writing 4 sqrt(2) and 3 sqrt(2) instead of sqrt(3)!!!!!!! I will go hang myself now. Sigh....
BTW great thinking. I take my hat off to you.
i made a different approach :( .great thinking :)
how you got the value of xy?
Log in to reply
draw a parallel to xy passing in Ob an draw a line from Ob to Oc. You will have a rectangle triangle with sides xy, 1 and 7
I did exactly the same but forgot the root when calculating XY and that ruined the whole thing
Yes. Same as yours.
can't understand till someone makes the graphic version.
1.solve it using circle of radius 3 cm and 4 cm touching each other. 2.take one of their common tangent. 3.take two point P,Q on tangent such that pair of tangents to respective circle make angle 60. 4. the triangle formed via three lines will be shortest equilateral triangle. 5. now u can easily solve it. a=4 tan(60) +4+3+ 3 tan(60)= 19.12
how did u calculated XY daniel?
add the diameter all of the circles, we will find 18, so the smallest side length of the equilateral triangle approximately 19
approximately?? And can you state the reasoning behind your 'solution,' as I can see no way of solving the problem using your 'solution'?
waaaaaaaaaaaaaaaaaaaaaaaaaaw!
That is a correct approach
? 2+3+4*2=20 not 18!!!!
tan 60° ×(4+3)+4+3 = ans
First, let the centers of the circles with radius 2 , 3 , 4 be O a , O b , O c respectively. Also, let the vertices of the equilateral triangle be A , B , C . Suppose that circle O c is tangent to A C and B C ; and circle O b is tangent to A B and B C .
Drawing the line of symmetry C O c , we see that if we can fit the circle O b at the place it is, we can fit a similar circle that is tangent to A C and A B , with the same radius. Therefore, the actual O a with radius 2 , can fit in the remaining space with no question; we need only to consider O b and O c .
To minimize the space taken, we let O b and O c be tangent. In addition, let the points of tangency of O b , O c to B C be X , Y , respectively. We can see from 3 0 − 6 0 − 9 0 triangles that C Y = 4 3 and B X = 3 3 . Also, X Y = ( 4 + 3 ) 2 − ( 4 − 3 ) 2 = 4 3 . Therefore, B C = 1 1 3 ≈ 1 9 . 0 5 , as desired.
As a side note, I don't really think that this problem should be in this set... Perhaps the Level 4 set would have been more appropriate, with the frustum cup filled with water problem replacing this in level 5.