Disease Test

Probability Level 1

A disease test is advertised as being 99% accurate: if you have the disease, you will test positive 99% of the time, and if you don't have the disease, you will test negative 99% of the time.

If 1% of all people have this disease and you test positive, what is the probability that you actually have the disease?

1% 50% 75% 99%

View wiki
Eli Ross by Eli Ross

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

6 solutions

Eli Ross Staff
Mar 8, 2016

You either don't have the disease and tested incorrectly ( 1 % × 99 % 1\% \times 99\% probability), or you don't have the disease and tested incorrectly ( 99 % × 1 % 99\% \times 1\% probability). By Bayes' Theorem, the probability you have the disease is 1 % × 99 % 1 % × 99 % + 99 % + 1 % = 50 % . \frac{1\% \times 99\%}{1\% \times 99\%+99\% + 1\%} = 50\%.

44 Helpful 0 Interesting 0 Brilliant 32 Confused

(You either don't have the disease and tested incorrectly) OR ( you don't have the disease and tested incorrectly) they both are essentially same statement, why are you adding this twice.

Do you mean to say: Since you test positive (You either have disease and tested correctly) OR ( You don't have the disease and tested incorrectly)

in which case it would be:

(1% X 99%) + (99% X 1%) = 2 X 99%. Thus 50% :)

Mayank Prasad - 4 years, 9 months ago

This is going to sound stupid, but why is it that when I put the equation above in a calculator, it gave me one percent?

Vercingetorix De Gaulle - 3 years ago

what is the probability one has the disease if they go for another test?

OM Das - 2 years, 12 months ago

If Im not mistaken there is a typo in your solution. It should be a multiply sign at the bottom not an add. i.e. 99%*1%

Thomas Kouroughli - 1 year, 11 months ago

d: having disease pos/neg:test result ^:not

p(d)=0.1 => p(^d)=0.9 p(pos|d)=0.99 => p(^pos|d)=0.01 p(neg|^d)=0.99 => p(pos|^d)=0.01

Bayes Theorem: p(d|pos)=p(pos|d) p(d)/p(pos) when p(pos)=p(d|pos)+p(^d|pos)=0.99 0.1 + 0.01 0.9=0.108 then p(d|pos)=(0.99 0.1)/0.108=0.917

Is this understanding of Bayes theorem right?

Farzad B - 1 year, 5 months ago

Isn't the denominator supposed to be 1% * 99% + 99% * 1% , not 1% * 99% + 99% + 1%

Saida Piri - 1 year, 1 month ago

Log in to reply

You are right, the denominator should be: 1% * 99% + 99% * 1%. That means the equation expression becomes: (99/10000)/(198/10000) = 50%.

Sergiu Bisceanu - 1 year ago

That should be little less than 50%

nikhil chandel - 4 years, 10 months ago

Log in to reply

why? It's exactly 50%.

Nikil K.R.P. - 2 years, 1 month ago
György Gehér
Apr 7, 2018

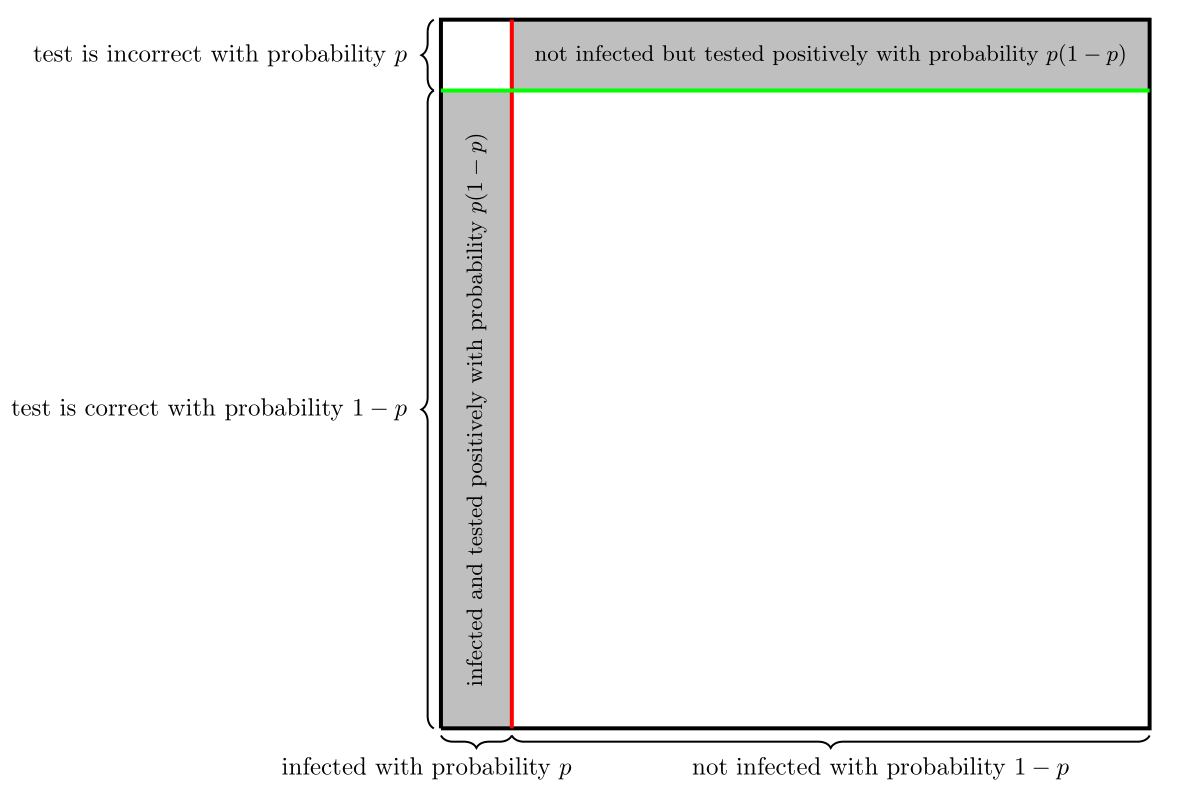
There is a certain symmetry which is worth mentioning here. From the figure below it is obvious that if the probability of being infected and tested incorrectly are the same (no matter how small they are), then the probability of being infected provided that tested positively is always 50%. From this figure it is also obvious that in order to increase this probability (so that the test would be actually useful), we have to increase the reliability of our test.

11 Helpful 4 Interesting 1 Brilliant 1 Confused

Very nice visualization

David Hastie - 2 years, 5 months ago

P(A) = probability of testing +ve P(B) = probability of disease

Given, P(B) = 1/100 P(A|B) = 99/100 (Probability that a person has disease and tests positive)

We have to find P(B|A) which is probability that you have a disease given you test positive

Using Bayes: P(B|A) = P(B) x P(A|B) /P(A) -----> Equation 1

we know P(B) and P(A|B) Only have to find P(A) Let C be event of probability of no disease. So, P(C) = 1- 1/100 = 99/100 and given in the problem is the fact that in case of no disease, the probability is 99/100 times accurate.. so 99/100 times it will correctly classify people with no disease as having no disease but incorrectly classify 1/100 times that people with no disease have disease. Let this be called P(D)

Now, probability of testing positive P(A) = probability of testing positive when when it is true + probability of testing positive when not true = 1/100 x 99/100 ( this is P(B) x P(A|B) ) + 99/100 x 1/100 (This is P(C) x P(D) ) = 2x 99/10000

substitute in Equation 1 above and solve.. answer= 1/2 or 50%

Ad C - 2 years, 1 month ago
Omer Nahum
Jun 12, 2020

(Chances for an incorrect result) * healthy people = 1% * 99 = 0.99

(Chances for correct result) * ill people = 99% * 1 = 0.99

Total positive results: 0.99 + 0.99 = 1.98

The probability for an ill person to test positive is:

(total ill persons) / (total positive tests): 0.99 1.98 \frac{0.99}{1.98} =50%

2 Helpful 0 Interesting 0 Brilliant 0 Confused
Eye Das
Jan 27, 2020

did it somewhat mechanically and got it right - this is an eye-opener man!

0 Helpful 0 Interesting 0 Brilliant 0 Confused
Daniyal Khawaja
Sep 15, 2019

There is a typo in Eli Ross's solution. Denomination should have a multiplication sign instead of a plus sign between the latter 99% and 1%.

CURRENTLY: ...+ 99% + 1%

SHOULD BE: ...+ 99% × 1%

0 Helpful 0 Interesting 0 Brilliant 0 Confused
Trini Moreno
Mar 30, 2017

You either don't have the disease and tested incorrectly ( probability), or you don't have the disease and tested incorrectly ( probability). By Bayes' Theorem, the probability you have the disease is

0 Helpful 0 Interesting 0 Brilliant 0 Confused

My solution: (sensitivity * probability of being infected)/((probability of being infected) sensitivity) (probability of not being infected)*(1- sensitivity)) where sensitivity is total cases when I was tested positive and I was actually infected. Hope this helps.

varun verma - 2 years, 2 months ago

why is it not : (0.01 x 0.99) / (0.01x0.99+ 0.01x 0.01) = 0.99 (99%) ?? I'm just referring to the bayes' theorem.

Alie Tan - 2 years ago

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...