Disintegrated Disk Debris

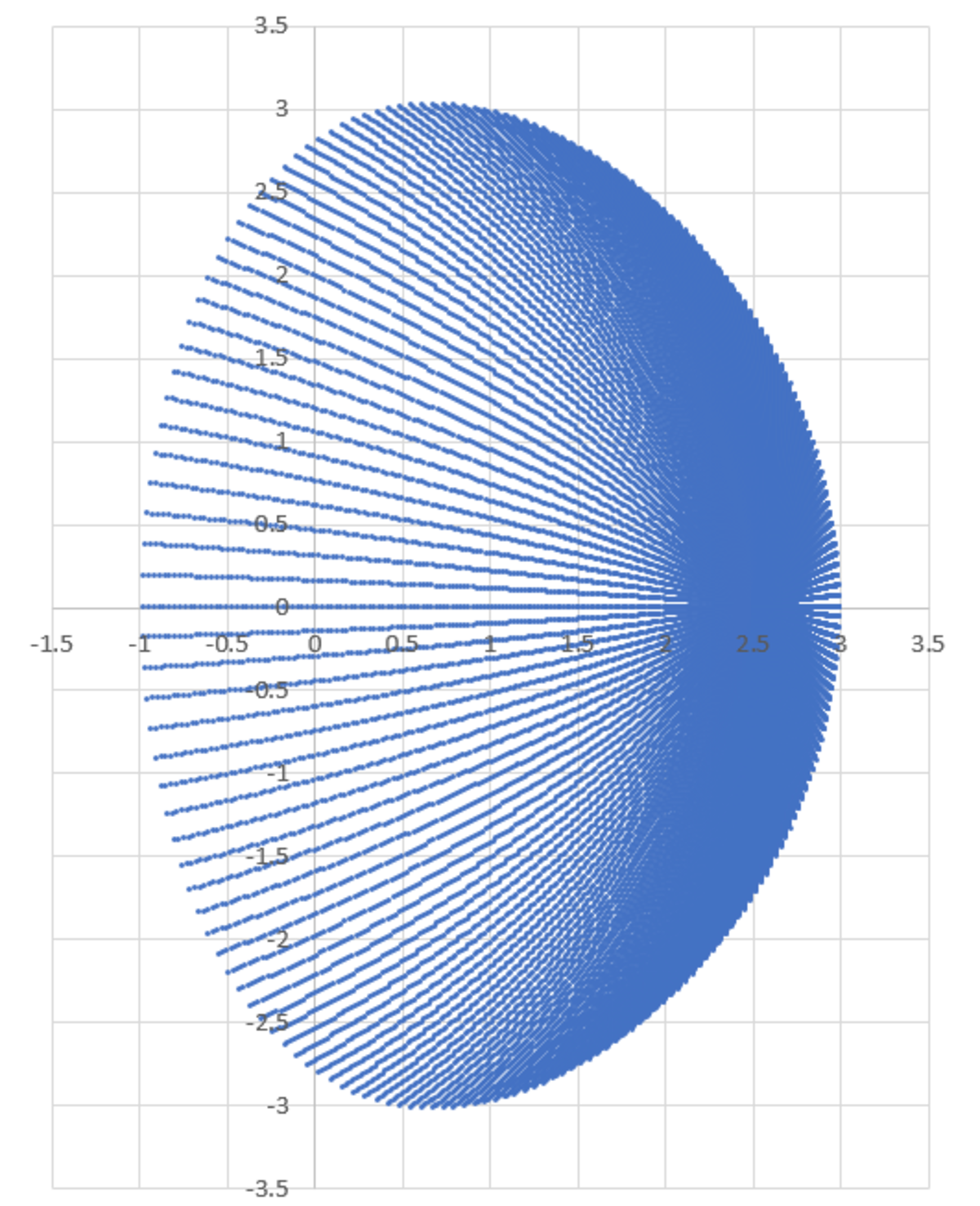
General outline of the solution: Consider a mass element of mass $dm = \rho r dr d\theta$ . It has an initial position:

$\vec{P}_d = r\cos{\theta} \hat{i} + r\sin{\theta} \hat{j}$

Let:

$\vec{n} = \vec{P}_d - \vec{P}$ $\hat{n} = \frac{\vec{P}_d - \vec{P}}{\mid \vec{P}_d - \vec{P} \mid}$

The initial velocity vector of this mass element is:

$\vec{v}_o = v_{ox} \hat{i} +yv_{oy} \hat{j}+v_{oz} \hat{k} = v_o \hat{n}$

The acceleration vector of this elementary mass is:

$\vec{a} = -g \hat{k}$

Solving for the motion of the element mass yields:

$x(t) = v_{ox}t + r\cos{\theta}$ $y(t) = v_{oy}t + r\sin{\theta}$ $z(t) = v_{oz}t -\frac{1}{2}gt^2$

When the mass strikes the XY plane again, it does so when $z = 0$ . This occurs at a time:

$T = \frac{2v_{oz}}{g}$

Using this, the x and y coordinates of landing can be found by replacing time $T$ in $x(t)$ and $y(t)$ . Let the final coordinates after flight be $X$ and $Y$ . Using these exact results, the moment of inertia of this mass element about the Z-axis can be found as such:

$dI = dm(X^2 + Y^2)$ $I = \int_{0}^{1}\int_{0}^{2\pi} (X^2 + Y^2) \rho r dr d\theta$

Substituting all expressions and simplifying gives the exact integrand. One may attempt to get a closed-form solution (not checked), but I have integrated this expression numerically to obtain:

$\boxed{\frac{I}{I_o} \approx 14}$

See the solution by @Karan Chatrath for details. Below is a picture of the debris field. To make this image, I divided the disk into $4 \times 10^4$ pieces and plotted the landing coordinates for all of them. I used a much higher resolution to derive the moment ratio. The bulk of the matter forms a crescent pattern on the right. The banding is an artifact of the finite resolution used to divide the disk.