Disorganized Pinwheel
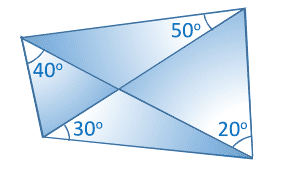
A quadrilateral has angles between its diagonals and sides as shown. Find the smaller of the two angles between the diagonals. If there are multiple solutions, report their average.
Note: Image not to scale.
The answer is 55.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Start labeling one of the unknown angles x and expressing the rest of the unknown angles in terms of x , as done in the figure above. Apply the law of sines to all the small triangles to get:
s i n ( 3 0 ) a = s i n ( x ) b
s i n ( 1 3 0 − x ) a = s i n ( 2 0 ) d
s i n ( 1 1 0 − x ) c = s i n ( 4 0 ) b
s i n ( 5 0 ) c = s i n ( x − 2 0 ) d
Solve for d b to get:
d b = s i n ( 2 0 ) s i n ( 1 3 0 − x ) × s i n ( 3 0 ) s i n ( x ) = s i n ( x − 2 0 ) s i n ( 5 0 ) × s i n ( 1 1 0 − x ) s i n ( 4 0 )
Equation on the right has five solutions, but only two of those are positive. They are x = 3 0 ∘ and x = 1 0 0 ∘ . They correspond to acute angles between the diagonals of 6 0 ∘ and 5 0 ∘ .