Displacement = Distance Not all the Time!!!!!!

A particle moves along a horizontal path, such that its velocity is given by v = $(3{ t }^{ 2 }-6t)$ m/s, where t is the time in seconds. If it is initially located at the origin O, determine the average speed during t = 0 to t = 3.5.(in m/s)

$Avg.\quad speed\quad =\quad \frac { total\quad distance }{ total\quad time }$ $v\quad =\quad 3{ t }^{ 2 }-6t\quad \\ v\quad =\quad 0\quad at\quad t\quad =\quad 2s$ For t < 2 s, velocity is -ve. At t = 2s, velocity is zero and for t > 2 s velocity is +ve. $\therefore \quad \quad \quad \quad { s }_{ 1 }\quad =\quad \int _{ 0 }^{ 3.5 }{ vdt } \quad =\quad \int _{ 0 }^{ 3.5 }{ (3{ t }^{ 2 }-6t)\quad dt } \\ \quad \quad \quad \quad \quad \quad \quad \quad =\quad 6.125\quad m\\ \quad \quad \quad \quad \quad \quad \quad \quad =\quad displacement\quad upto\quad 3.5\quad s\quad \\ \quad \quad \quad \quad \quad { s }_{ 2 }\quad =\quad \int _{ 0 }^{ 2 }{ vdt } \quad =\quad \int _{ 0 }^{ 2 }{ (3{ t }^{ 2 }-6t)\quad dt } \\ \quad \quad \quad \quad \quad \quad \quad \quad =\quad -4\quad m\quad \\ \quad \quad \quad \quad \quad \quad \quad \quad =\quad displacement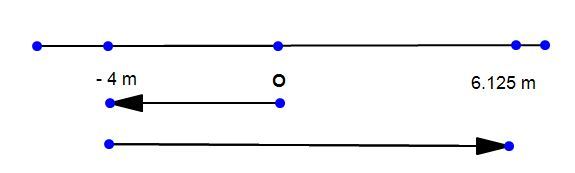\quad upto\quad 2s$ image d = distance traveled in 3.5s

= 4 + 4 + 6.125

= 14.125.