Distance Around a Parallelogram
A B C D is a parallelogram. E is a point on D C extended, such that D and E are on opposite sides of B C . Let A E intersect B C and B D at F and G , respectively. If A G = 1 8 0 and F G = 1 0 8 , what is E F ?
The answer is 192.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
14 solutions
Every solution approach this using similar triangles from Property D of parallel lines . This solution is the cleanest and most direct. Every other solution required more work in chasing angles and ratios.
It is interesting to note that G A 2 = G F ⋅ G E . What is the simplest way of showing this?
Note that when writing out similar triangles, it is extremely helpful to ensure that your vertices match up properly. This will make it extremely easy to write down the ratios.
Log in to reply
Hi Calvin. Is it possible to solve this problem using mass point geometry?
tr.BGF ~ tr.DGA
So, GF/GA=BF/AD 108/180=BF/AD BF=3/5AD
So, BF=3/5BC Also, CF=2/5BC
CF/BF=2/3
tr.FEC ~ tr.FAB
FE/FA=CF/BF FE/288=2/3 FE=192 So, EF =192
Due to the fact A B ∥ D E , we have:
∠ B A G = ∠ D E G , ∠ A B G = ∠ G D E , which implies △ A B G ∼ △ E D G .
∠ A B F = ∠ E C F , ∠ B A F = ∠ C E F , which implies △ A B F ∼ △ E C F .
Therefore A G E G = A B E D and A F E F = A B E C
Note E G = 1 0 8 + E F , A G = 1 8 0 , A F = 1 8 0 + 1 0 8 = 2 8 8 and E D = E C + C D = E C + A B .
Thus, 1 8 0 1 0 8 + E F = A B E C + A B and 2 8 8 E F = A B E C .
Subtracting 1 from the first equation, we get: 1 8 0 1 0 8 − 1 8 0 + E F = A B E C
Replacing A B E C with 2 8 8 E F for that equation, we get: 1 8 0 E F − 7 2 = 2 8 8 E F
( E F − 7 2 ) × 2 8 8 = E F × 1 8 0
E F × 2 8 8 − 2 0 7 3 6 = E F × 1 8 0
E F × ( 2 8 8 − 1 8 0 ) = 2 0 7 3 6
E F × 1 0 8 = 2 0 7 3 6
Thus E F = 1 0 8 2 0 7 3 6 = 1 9 2 .
Let $x$ be the length of side $\overline{EF}$. Since triangles $\Delta ECF$ and $\Delta EDA$ are similar, we see that $\frac{x}{108+180+x}=C$ where $C$ is the constant of proportionality between the two triangles. Let $y$ be the length $\overline{AD}$, and let $t$ be the length $\overline{BF}$, and we see that we also have that $\frac{y-t}{y}=C$. Using the similarity of the triangles $\Delta GBF$ and $\Delta GDA$, we see that $\frac{t}{y}=\frac{108}{180}$, and so $C=1-\frac{108}{180}=\frac{72}{180}$. Solving the equation $\frac{x}{288+x}=\frac{72}{180}$, we obtain the final answer $x=192$.
Let EF be x . Let AB be a and CE be b .
Since triangle CEF and triangle BAF are similar, 1 8 0 + 1 0 8 x = a b .
Since triangle ABG and triangle EDG are similar, 1 8 0 x + 1 0 8 = a a + b = 1 + a b .
Therefore, from the 2 equations, we get:
2 8 8 x + 1 = 1 8 0 x + 1 0 8
So, 1 8 0 x + 1 8 0 ⋅ 2 8 8 = 2 8 8 x + 1 0 8 ⋅ 2 8 8
1 0 8 x = 7 2 ⋅ 2 8 8
x = 1 9 2 and we are done.
from the given picture we see that triangle DEG & triangle AGB are similar. therefore GE/DE = AG/AB ..........(1). from triangle ADE & triangle FCE we get AE/FE = DE/CE ............(2).(since triangle ADE & triangle FCE are similar.) from triangle ABF & CFE we get AF/FE = AB/CE ...........(3).(since triangle ABF & triangle CFE are similar.) now from (2) we get DE = AE x CE/FE . from (1) we get FExGE/AExCE = AG/AB (putting the value of DE in (1).) therefore AB/CE = AExAG/FExGE . from (3) we get AF/FE = AExAG/FExGE . therefore AF/AG = AE/GE. therefore AFxGE = AExAG or, AFx(GF+FE) = (AF+FE)xAG or, AFxGF+AFxFE = AFxAG+FExAG . or, AFxFE - FExAG = AFxAG - AFxGF or, FEx(AF-AG) = AFx(AG-GF) or, FExGF = (AG+GF)x(AG-GF) or, FE= (AG^2 - GF^2)/GF since AG = 180 , GF=108 therefore, FE =(180^2-108^2)/108=192
A D ∥ B C with transversal A E ⇒ ∠ D A E ≅ ∠ B F A (1)
A B ∥ D E with transversal A E ⇒ ∠ A E D ≅ ∠ F A B (2)
A D ∥ D E with transversal D B ⇒ ∠ A D G ≅ ∠ F B G (3) and ∠ E D G ≅ ∠ A B G (4)
1 and 2 ⇒ △ D A E ∼ △ B F A
1 and 3 ⇒ △ D A G ∼ △ B F G
2 and 4 ⇒ △ D G E ∼ △ B G A
By properties of similar triangles: F G A G = A G E G A G = 1 8 0 , F G = 1 0 8 , E G = F G + F E = 1 0 8 + F E 1 0 8 1 8 0 = 1 8 0 1 0 8 + F E ⇒ F E = 1 9 2
A. Triangle ABG is similar to Triangle EDG. Therefore:
AB/AG = ED/EG AB/180 = (DC+EC)/(EF+FG) = (DC+EC)/(EF + 108) AB/180 = (AB + EC)/(EF + 108)
B. Triangle ABF is similar to Triangle ECF. Therefore:
AB/AF = EC/EF AB/288 = EC/EF
C. Triangle ECF is similar to Triangle EDA. Therefore:
EF/EC = EA/ED EF/EC = (EF+ 288)/(EC + CD) = (EF + 288)/ (EC + AB)
To conclude, we have three simultaneous equations relating three lengths:
AB/180 = (AB + EC)/(EF + 108)
AB/288 = EC/EF
EF/EC = (EF + 288)/ (EC + AB)
From here we can solve to obtain the length EF, which is 192 in this case.
As B D and A F are diagonals of the quadrilateral A B F D meeting at G , [ F B D ] [ A B D ] = F G A G = 1 0 8 1 8 0 = 3 5 Letting [ A B D ] = 5 x , we obtain [ F B D ] = 3 x and [ B C D ] = 5 x so [ F C D ] = [ B C D ] − [ F B D ] = 2 x thus F C B F = [ F C D ] [ F B D ] = 2 3 As A B / / C E , A B F is similar to C E F so E F A F = F C B F = 2 3 and since A F = A G + G F = 2 8 8 we can calculate that E F = 1 9 2
AD/FC=AE/EF=(288+EF)/EF and AD/BF=AD/(AD-FC)=AG/GF=180/108
Firstly, you should construct a diagram. Make sure the diagram is accurate, or you will be confused. The next step is to identify some similar triangles to compare ratios. Then, you are done. After drawing the diagram, we can identify that Triangle FEC is similar to Triangle ABF.
So, we claim that FEC is similar to ABF
Proof:
Using the formula AAA( Angle-Angle-Angle), we can prove that FEC is similar to ABF as ∠ C F E = ∠ A F B because of the opposite angle theorem, ∠ F C E = ∠ A B F because they are alternate interior angles formed by two parallel lines. Lastly, ∠ F A B = ∠ F E C because they are also alternate interior angles formed by two parallel lines. QED
Now, we will name line segment AB d, line segment CE z, and line segment FE c.
We will now claim another two triangles are similar,
Claim Triangle AGB is similar to Triangle DGE
Proof:
Using AAA, we can see that ∠ D G E = ∠ A G B because of the opposite angle theorem, ∠ G E D = ∠ G A B because of the alternate interior angles formed by two parallel lines. Lastly, ∠ G D E = ∠ A B G because the other angles of the triangles are the same.QED
Now, we can form the two equations that will solve the question.
z c = d 2 8 8 (1)
d + z d = 1 0 8 + c 1 8 0 (2)
The first equation is quite obvious.
z c = d 2 8 8 because of the ratio between Triangle FEC and Triangle AFB.
The second equation is actually not ambiguous too.
d + z d = 1 0 8 + c 1 8 0 because of the ratio between Triangle AGB and Triangle DGE.
Usually, an equation with 3 variables is quite impossible to solve without 3 equations. But this counts as a very special case.
By cross-multiplication, we get
( 1 0 8 + c ) d = 1 8 0 ( d + z ) from (2)
We get c d = 2 8 8 z from (1)
By substitution, we get (3)
3 z = 2 d (3)
Then, we substitute (3) into (2),
We will get c=192 and we are done.
By property D in Parallel Lines , triangles G F B and G A D are similar so G A G F = G D G B . Likewise, triangles G E D and G A B are similar, so G A G E = G B G D . Multiplying these equations together, we get G A G F ⋅ G A G E = G D G B ⋅ G B G D = 1 , hence A G 2 = E G ⋅ F G . This gives G E = F G A G 2 = 1 0 8 1 8 0 2 = 3 0 0 . Thus F E = G E − G F = 3 0 0 − 1 0 8 = 1 9 2 .
We can note by AA criteria that △ B G F and △ D G A are similar, therefore,
D A B F = G A G F = 1 8 0 1 0 8 = 5 3
[Note that DA = BC]
Next, △ A F B and △ E F C are similar, therefore,
E F A F = F C F B = 2 3 [from above ratio of 5 3 ]
E F 1 8 0 + 1 0 8 = 2 3
EF =192
NOTE: It is very important to write the correct corresponding vertices of triangles when mentioning similarity, which makes writing the ratio of sides very easy.
You should not JUST write the name of triangles; but also write them in correct vertices' order!!
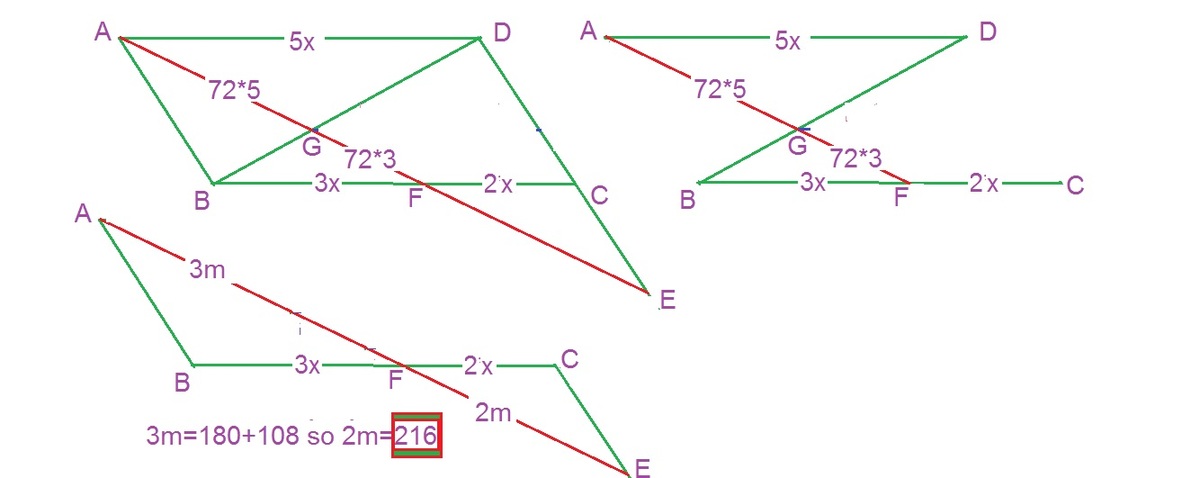
Since A D ∥ B C , △ A D G ∼ △ B F G by AA similarity.
Likewise, △ A B F ∼ △ E D A
A G : G F = 1 8 0 : 1 0 8 = 5 : 3 , thus by similarity, A D : B F = 5 : 3 and A E : A F = 5 : 3
A F = 2 8 8 , so A E = 4 8 0
E F = A E − A F = 4 8 0 − 2 8 8 = 1 9 2