Distance Between Incenters

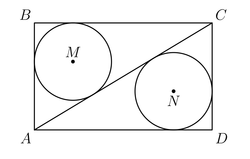Level 2

Let $ABCD$ be a rectangle such that $AB=5$ and $BC=12$ . Suppose that $M$ and $N$ are the centers of the circles inscribed inside triangles $\triangle ABC$ and $\triangle ADC$ respectively. What is $MN^2$ ?

The answer is 65.

3 solutions

Faraz Masroor
Mar 28, 2014

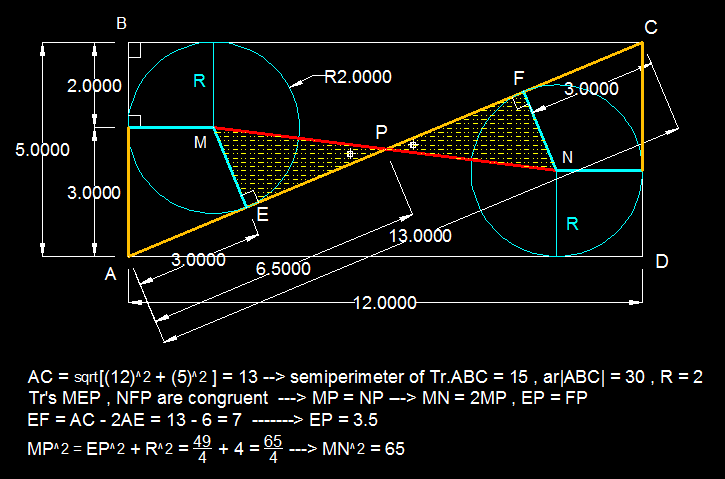
Finally a geometry problem on this site! Let X b e the midpt of AC. Then MN=2XN by symmetry. Using coordinates, X=(6, 5/2) and N you can find is (10,2) since AC=13 and s=15, you can find the length f the tangent from A is 15-5=10 and the height of N from the Xaxis (AD) is the inradius 2. Then you can use the distance formula to see that XN=1/2 sqrt65 so MN=sqrt 65, so the answer is 65.

(Y)

Muhammed Anäs - 7 years, 2 months ago

Kaveesh Kulkarni
May 30, 2019

AC^2 = 12^2 + 5^2 , \therefore , AC = 13. Let MF \perp AC MF = r Let NE \perp AC NE = r \therefore NE \parallel MF. As, NE = MF NE \parallel MF \Box MFNE is a parallelogram. Let EF \bigcap MN = {O} EO = FO MO = NO . As \odot M is incircle , AF = s - a \therefore AF = 3 . \triangle ABC \cong \triangle CDA. AF = CE \therefore CE = 3. EF = 13 - 6 EF = 7 FO = 3.5. [ABC] = r \times s. 12 \times 5 ÷ 2 = r \times 15 30 = r \times 15 r = 2. \therefore MO^2 = FO^2 + MF^2. MO^2 = 12.25 + 4 MO^2 = 16.25 MO = 4.0311.... MN = 8.0622.... MN^2 = 64.9997..... MN^2 \approx 65 .

Ahmad Saad
Mar 13, 2017

How did you find AE = 3?

Kaveesh Kulkarni - 2 years ago

Distance Between Incenters

The answer is 65.

3 solutions

0 pending reports