Distance between points on a curve
Take a look at the following picture.
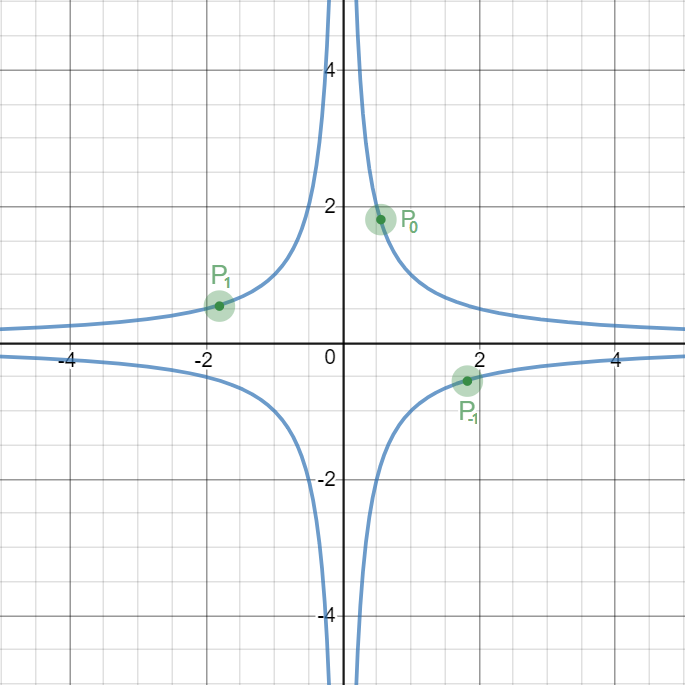
In this picture you can see the graph of the curve x 2 y 2 = 1 . Let P 0 be a point on the curve in the first quadrant. Furthermore, define for k ∈ { − 1 , 1 } , P k as the point P 0 rotated around O by 2 k π . Notice that P k lies on the curve as well, independent of the choice of P 0 .
There are two values of P 0 , say Q 1 and Q 2 , on the curve in the first quadrant such that the line through P 0 , tangent to the curve intersects the curve at P − 1 or P 1 . The (Euclidean) distance of those two points can be written as d ( Q 1 , Q 2 ) = a + b c , where a , b , c ∈ Z , such that c is prime. Find c a b .
The answer is -8.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
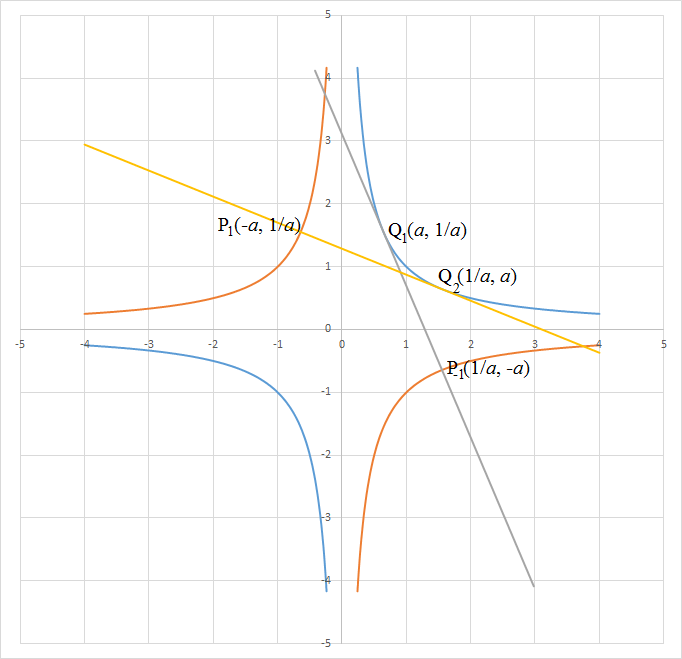
The curve x 2 y 2 = 1 ⟹ y = ± x 1 . The blue curves in the first and third quadrants are y = x 1 , while the orange curves in the second and fourth quadrants are y = − x 1 .
Let Q 1 in the first quadrant be ( a , a 1 ) . Then its corresponding P − 1 is ( a 1 , − a ) . The gradient of the line Q 1 P − 1 , m = a − a 1 a 1 + a = a 2 − 1 a 2 + 1 . Since Q 1 P − 1 is also the tangent of y = x 1 at Q 1 , then m = d x d y = − x 2 1 at Q 1 or m = − a 2 1 .
Then we have:
a 2 − 1 a 2 + 1 a 4 + 2 a 2 − 1 ⟹ a 2 a ⟹ a 1 = − a 2 1 = 0 = 2 − 1 = 2 − 1 = 2 − 1 1 = 2 + 1 Since a 2 > 0
And Q 1 ( 2 − 1 , 2 + 1 ) . Since y = x 1 is symmetrical about y = x , Q 2 has its x -coordinate and y -coordinate swapped with those of Q 1 or Q 2 ( 2 + 1 , 2 − 1 ) .
Therefore,
d ( Q 1 , Q 2 ) = ( 2 − 1 − 2 + 1 ) 2 + ( 2 + 1 − 2 − 1 ) 2 = 2 ( 2 − 1 − 2 ( 2 + 1 ) ( 2 − 1 ) + 2 + 1 ) = − 4 + 4 2
⟹ c a b = 2 − 4 × 4 = − 8 .
The curve in the first quadrant follows the equation y = x 1 , and using a derivative the slope of that curve at any point P 0 ( p , p 1 ) is y = − p 2 1 , so the tangent line to any point P 0 ( p , p 1 ) on the curve is y = − p 2 1 x + p 2 .
By rotational symmetry, P − 1 is at ( p 1 , − p ) , and since this point is also on the tangent curve, we have − p = − p 2 1 ⋅ p 1 + p 2 which solves to p = − 1 + 2 .
Therefore, P 0 , or Q 1 , is ( − 1 + 2 , − 1 + 2 1 ) , and by symmetry, Q 2 is ( − 1 + 2 1 , − 1 + 2 ) , which makes the distance d ( Q 1 , Q 2 ) = − 4 + 4 2 , so a = − 4 , b = 4 , and c = 2 , and c a b = − 8 .