Distance is not perpendicular
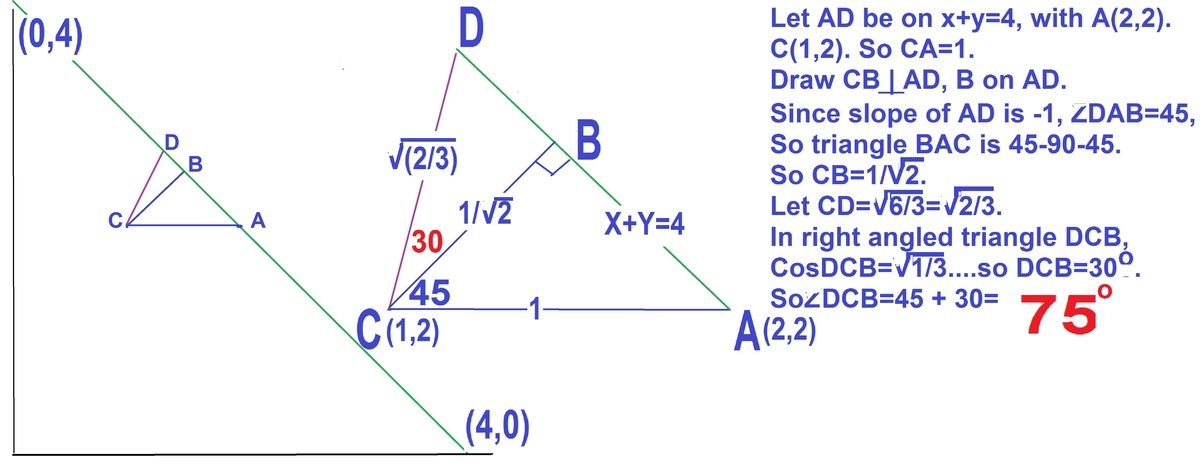
A straight line L passes through ( 1 , 2 ) and intersects the line x + y = 4 at a distance 3 6 from ( 1 , 2 ) .
Over all possible L , what is the largest acute angle, in degrees, that the line L makes with the x -axis?
The answer is 75.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Use the parametric form of a straight line,
c
o
s
θ
x
−
1
=
s
i
n
θ
y
−
2
=
3
6
.
By putting values of
x
and
y
in
x
+
y
=
4
we get
θ
=
1
5
°
or
7
5
°
. The greater is
7
5
°
. So, answer is
7
5
°
x + y = 4 or y = 4 - x (eqn 1)
Consider a circle centered at ( 1 , 2 ) with radius = sqrt(6)/3. It's equation will be (x - 1)^2 + (y -2)^2 = 6/9. (eqn 2) and it touches eqn 1 at 2 points.
Substitute 4 - x for y in eqn 2, then expand.
x^2 - 2x + 1 + 4 - 4x +x^2 = 2 / 3
Solving the quadratic yields x = 1.7875 or 1.2125. Use the second value as that makes the line through (1,2) steeper and thus the bigger angle with x - axis.
y = 4 - 1.2125 or y = 2.7875 which yields a slope of that line (2.7875 -2 ) / ( 1.2125 - 1) = .7875 / .2125 = 3.7059
tan^-1(3.7059) = 74.899 degrees or 75 degrees
the larger angle with x axis must be 105 degrees