Distance moved till rolling.
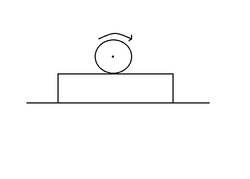 A horizontal plank having mass
m
lies on a smooth horizontal surface. A sphere of same mass and radius
R
is spined to an angular frequency
ω
and gently placed on the plank. If coefficient of friction between the plank and the sphere is
μ
, find the distance moved by the plank till the sphere starts pure rolling on the plank. The plank is long enough.
If answer is of the form
b
a
μ
g
ω
2
R
2
, find
a
+
b
where
a
and
b
are two co-primes integers.
A horizontal plank having mass
m
lies on a smooth horizontal surface. A sphere of same mass and radius
R
is spined to an angular frequency
ω
and gently placed on the plank. If coefficient of friction between the plank and the sphere is
μ
, find the distance moved by the plank till the sphere starts pure rolling on the plank. The plank is long enough.
If answer is of the form
b
a
μ
g
ω
2
R
2
, find
a
+
b
where
a
and
b
are two co-primes integers.
The answer is 83.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
I didn't consider psuedo force instead I took 2v=rω Is that a problem? Can you please tell when to take psuedo forces
Log in to reply
As you can see that we are analyzing the motion of sphere wrt planck and as our initial frame(planck) is too moving therefore, we have to apply pseudo force.
Log in to reply
why do we have to make the plank the frame of reference? Why not an inertial frame of reference?
In the method i did i took a( sphere) =5/2μg and a(plank)=μg so a(relative)=7/2μg . Can u pls help where i am wrong
I feel as if this is the distance traveled by the plank with respect to the sphere instead of the distance traveled by the plank with respect to an inertial reference frame.
Let's consider the forces acting on the sphere and the block individually. First of all, we note that as the sphere rolls, the bottom most point is travelling to the left, so friction on the sphere will be acting to the right. Clearly, an equal and opposite force will be acting to the left on the plank. We can set up the equations of motion for both systems:
I α = F f R = m g μ R m a = F f = m g μ m A = − F f = − m g μ
where a is the translational acceleration of the sphere, A is the acceleration of the plank, and α is the angular acceleration of the sphere.
We are interested in the time at which the sphere rolls without slipping with respect to the plank. If we let the translational velocity of the sphere be v and the velocity of the plank be V , then the velocity of the sphere with respect to the plank is v − V , so we wish to compute the time at which:
ω = R v − V
where ω is the angular velocity of the sphere. Since the acceleration is constant, we then will have:
ω = ω 0 − α t = ω 0 − I m g μ R t V = A t = − m g μ t v = a t = m g μ t
which gives us:
ω 0 − I m g μ R t = R 2 m g μ t ⇒ ( R 2 g μ + I m g R μ ) t = ω 0 ⇒ t = 9 g μ 2 R ω 0
as a sphere's moment of inertia is given by I = 5 2 m R 2 . Finally, in the case of constant, acceleration, the distance that the plank travels is given by:
D = 2 1 ∣ a ∣ t 2 = 2 1 g μ ( 9 g μ 2 R ω 0 ) 2 = 8 1 g μ 2 R 2 ω 0 2
So we will have:
a = 2 , b = 8 1 ⇒ a + b = 2 + 8 1 = 8 3
Let the ball be given angular velocity ω in *clock wise * direction.
Consider k in the diagram as μ Let us fix our frame of reference with the moving wedge. As it is a non-inertial frame so we have to apply pseudo force on the sphere. As the acceleration of the plank is μ g towards left so pseudo force acting on the ball is μ m g in right ward direction.
Acceleration of the CoM of theball ( a ) = 2 μ g
Let us assume that the ball starts pure rolling motion after time t .
So velocity of CoM of the ball after timr t is 2 μ g t
Let the angular velocity of the ball be ω 0 when it starts pure rolling motion.
So R ω 0 = 2 μ g t .................(1)
Now torque acting on the ball the CoM is μ m g R
So
I α = μ m g R
Note that the directions of the angular velocity and the angular acceleration are opposite.
Putting I = 5 2 m R 2
we get α = 2 R 5 μ g
Now
ω 0 = ω + ( − α t )
Putting the values in this equation we get
t = 9 μ g 2 R ω
Now distance moved by plank ( S ) is 0 . 5 a t 2
So S = 8 1 μ g 2 R 2 ω 2