A Triangle Problem

The distances of a point from the vertices of an equilateral triangle are 3 , 5 , 7 . The point lies in the plane of the triangle and outside the triangle.
If the side length of the equilateral triangle is s . Find s 2
The answer is 19.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
8 solutions
Brilliant. By implementating Pompeiu's theorem one solves the problem in a similar manner (in addition to the cosine rule of course).
Let the coordinate of the three vertices of the equilateral triangle be ( 0 , 2 3 s ) , ( 2 1 s , 0 ) , and ( − 2 1 s , 0 ) , and the coordinates of the external point be P ( x , y ) . Then by Pythagorean theorem :
⎩ ⎪ ⎪ ⎨ ⎪ ⎪ ⎧ x 2 + ( y − 2 3 s ) 2 = 3 2 ( x − 2 1 s ) 2 + y 2 = 5 2 ( x + 2 1 s ) 2 + y 2 = 7 2 . . . ( 1 ) . . . ( 2 ) . . . ( 3 ) ⟹ ⎩ ⎪ ⎨ ⎪ ⎧ x 2 + y 2 − 3 s y + 4 3 s 2 = 9 x 2 − s x + 4 1 s 2 + y 2 = 2 5 x 2 + s x + 4 1 s 2 + y 2 = 4 9 . . . ( 1 ) . . . ( 2 ) . . . ( 3 )
⎩ ⎪ ⎨ ⎪ ⎧ ( 3 ) − ( 2 ) : 2 s x = 2 4 ( 3 ) − ( 1 ) : s x + 3 s y − 2 s 2 = 4 0 ⟹ x = s 1 2 ⟹ y = 3 s 2 8 + 2 3 s
Substitute x and y in ( 3 ) :
s 2 1 4 4 + 1 2 + 4 s 2 + 3 s 2 7 8 4 + 3 2 8 + 1 2 s 2 3 s 2 − 3 8 3 + 3 s 2 1 2 1 6 s 4 − 8 3 s 2 + 1 2 1 6 ( s 2 − 6 4 ) ( s 2 − 1 9 ) ⟹ s 2 = 4 9 = 0 = 0 = 0 = 1 9 Multiply both sides by 3 s 2
Note that s = 6 4 = 8 is unacceptable because the point P will be in the equilateral triangle.
subtle approach!
But sir won't there be 6 cases of connecting coordinates with distance formula, are the rest cases yielding no result??
Log in to reply
They all are either image reflections or rotational equivalents
I see what you mean Edward. The working has arbitrarily chosen which vertex is which distance from the point. Therefore the other points do not come up.
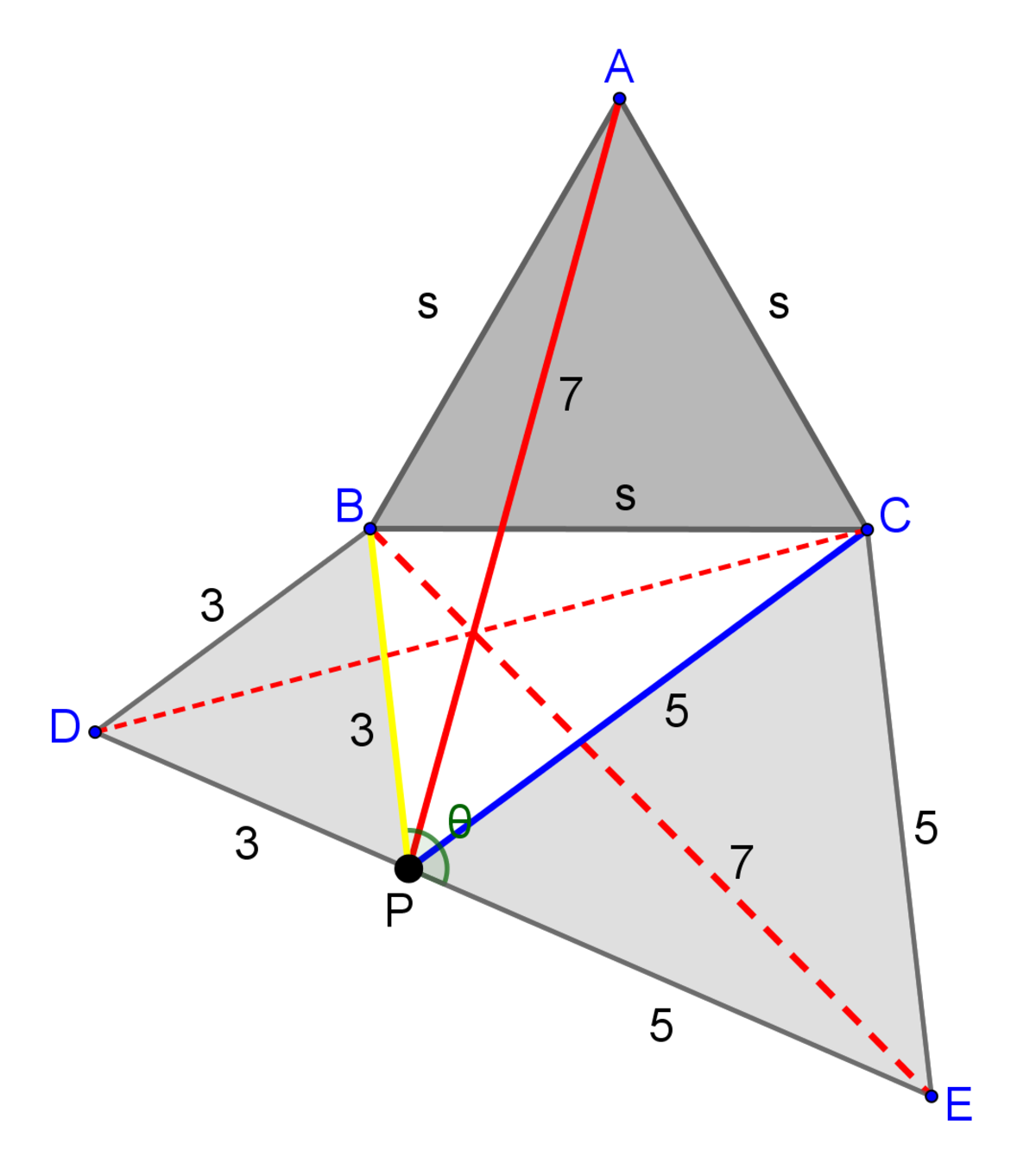 Let ABC be the given equilateral triangle and P the point who’s distances from the vertices of ABC are PA=7, PB=3 and PC=5. If we consider the equilateral triangles PBD and PCE outside BPC, we get the well-known figure where Fermat’s point occurs as the point where the red line segments concur. Now, these red segments are congruent, just because triangles ABP and CBD are congruent as well as triangles DPC and BPE are.
Hence, the sides of triangle BPE have lengths 3, 5 and 7. Using cosine rule on this triangle, we get:
B
E
2
=
P
B
2
+
P
E
2
−
2
⋅
P
B
⋅
P
E
⋅
cos
θ
⇒
cos
θ
=
2
⋅
P
B
⋅
P
E
P
B
2
+
P
E
2
−
B
E
2
=
2
⋅
3
⋅
5
3
2
+
5
2
−
7
2
=
−
2
1
⇒
θ
=
1
2
0
∘
⇒
∠
B
P
C
=
θ
−
∠
E
P
C
=
1
2
0
∘
−
6
0
∘
=
6
0
∘
Once again, by cosine rule, on triangle BPC this time, we have:
B
C
2
=
P
B
2
+
P
C
2
−
2
⋅
P
B
⋅
P
C
⋅
cos
(
∠
B
P
C
)
=
3
2
+
5
2
−
2
⋅
3
⋅
5
⋅
cos
6
0
∘
=
9
+
2
5
−
2
⋅
3
⋅
5
⋅
2
1
=
1
9
The answer is
s
2
=
1
9
Let ABC be the given equilateral triangle and P the point who’s distances from the vertices of ABC are PA=7, PB=3 and PC=5. If we consider the equilateral triangles PBD and PCE outside BPC, we get the well-known figure where Fermat’s point occurs as the point where the red line segments concur. Now, these red segments are congruent, just because triangles ABP and CBD are congruent as well as triangles DPC and BPE are.
Hence, the sides of triangle BPE have lengths 3, 5 and 7. Using cosine rule on this triangle, we get:
B
E
2
=
P
B
2
+
P
E
2
−
2
⋅
P
B
⋅
P
E
⋅
cos
θ
⇒
cos
θ
=
2
⋅
P
B
⋅
P
E
P
B
2
+
P
E
2
−
B
E
2
=
2
⋅
3
⋅
5
3
2
+
5
2
−
7
2
=
−
2
1
⇒
θ
=
1
2
0
∘
⇒
∠
B
P
C
=
θ
−
∠
E
P
C
=
1
2
0
∘
−
6
0
∘
=
6
0
∘
Once again, by cosine rule, on triangle BPC this time, we have:
B
C
2
=
P
B
2
+
P
C
2
−
2
⋅
P
B
⋅
P
C
⋅
cos
(
∠
B
P
C
)
=
3
2
+
5
2
−
2
⋅
3
⋅
5
⋅
cos
6
0
∘
=
9
+
2
5
−
2
⋅
3
⋅
5
⋅
2
1
=
1
9
The answer is
s
2
=
1
9
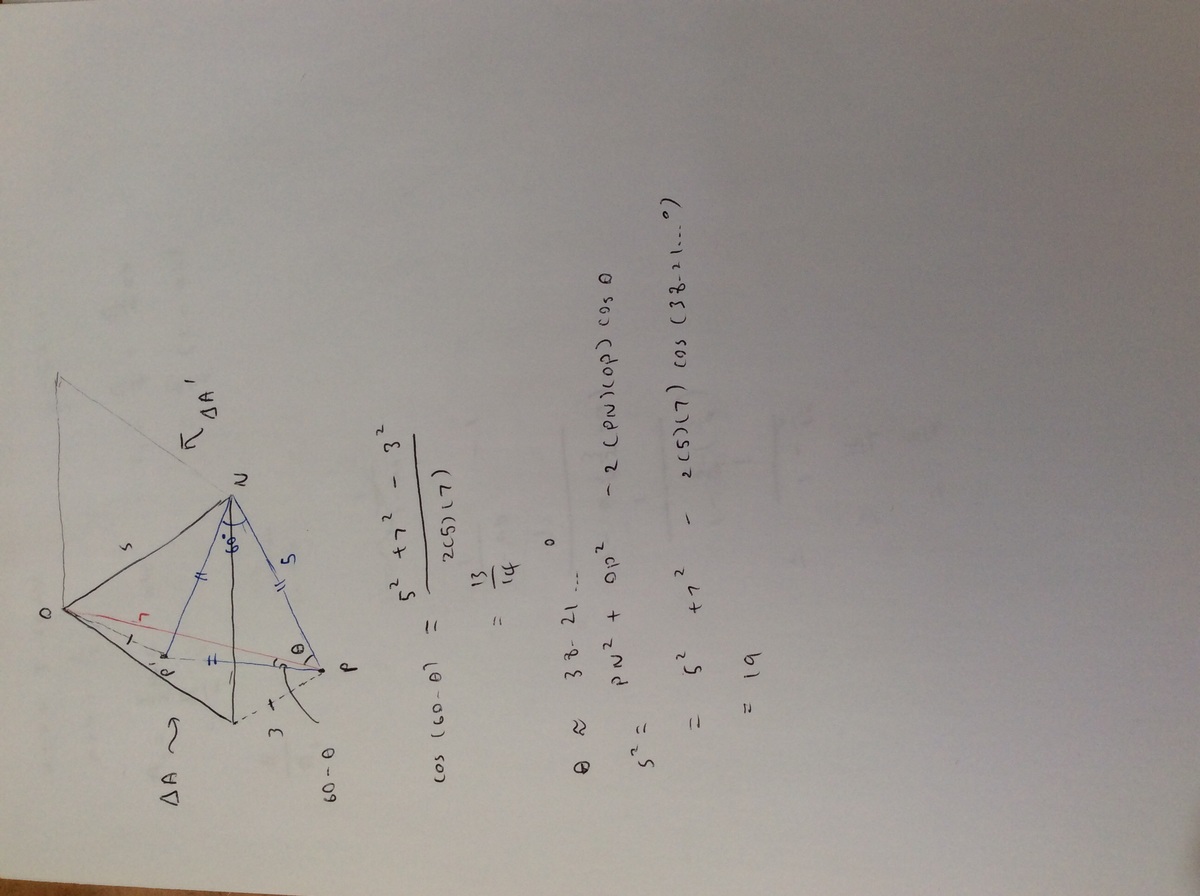
Note: triangle A' is obtained upon a 60 degrees clockwise rotation of triangle A; Theta is the angle ∠OPN
Inspiration: Coffin Problems
I use the Heron formula and create an equation adding in one side the areas for the triangles (s, 3, 7) and (s, 5, 7), and in the other side (s, s, s) and (s, 3, 5). Solving the equation there are other solution for s that is 6.4 and the square 40.96. I would like to understand why it is not accepted, am I doing something wrong?.
Log in to reply
Solve
(-sqrt((3+5+s)
(3+5-s)
(3-5+s)
(-3+5+s))+sqrt((3+s+7)
(3+s-7)
(3-s+7)
(-3+s+7))
+sqrt((s+5+7)
(-s+5+7)
(s-5+7)
(s+5-7))-sqrt(3)
s^2).
We get s=4.3589. 4.3589^2=19.
I used https://keisan.casio.com/calculator for do loop from 3-.1-20, 4-.1-10, 4.3-.01-10, 4.35-.001-10, 4.358-.0001-10
at 4.3589 the result was 0.
Use the relation 3(3^4+5^4+7^4+s^4)=(3^2+5^2+7^2+s^2)^2 Find, s^2=19 and 64. Choose the relevant Answer =19.

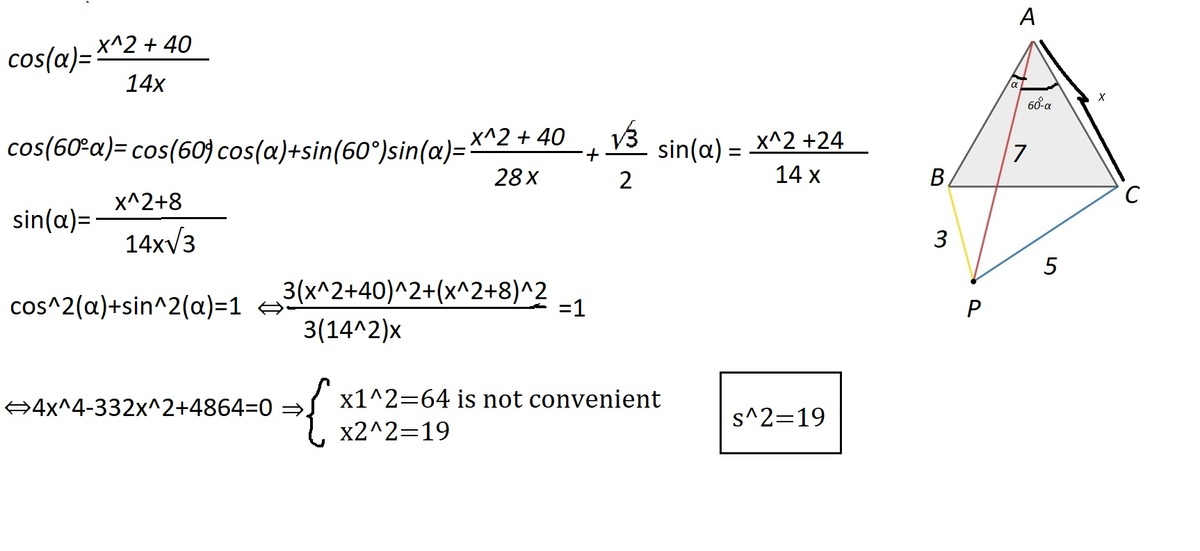
Label the equilateral triangle Q R S and label the point outside the triangle P , and rotate the whole diagram 6 0 ° counterclockwise about Q so that S goes to R , P goes to P ′ , and R goes to R ′ . Then R P ′ = S P = 3 , R ′ P ′ = R P = 5 , and Q P = Q P ′ = 7 .
Draw P P ′ . Since Q P = Q P ′ and ∠ P Q P ′ = 6 0 ° , △ P Q P ′ is an equilateral triangle and P P ′ = Q P = Q P ′ = 7 .
By the law of cosines on △ P R P ′ , ∠ P R P ′ = cos − 1 ( 2 ⋅ 3 ⋅ 5 3 2 + 5 2 − 7 2 ) = 1 2 0 ° .
By the angle sum of a triangle, ∠ R P P ′ + ∠ R P ′ P = 6 0 ° , and from equilateral triangle △ P Q P ′ , ∠ Q P ′ R + ∠ R P ′ P = ∠ Q P R + ∠ R P P ′ = 6 0 ° , and since △ Q P ′ R ≅ △ Q P S by SSS congruence, ∠ Q P S = ∠ Q P ′ R . Therefore, ∠ S P R = ∠ Q P S + ∠ Q P R = 6 0 ° .
Finally, by law of cosines on △ S P R , s 2 = 3 2 + 5 2 − 2 ⋅ 3 ⋅ 5 ⋅ cos 6 0 ° = 1 9 .