Distinct consecutive sums!

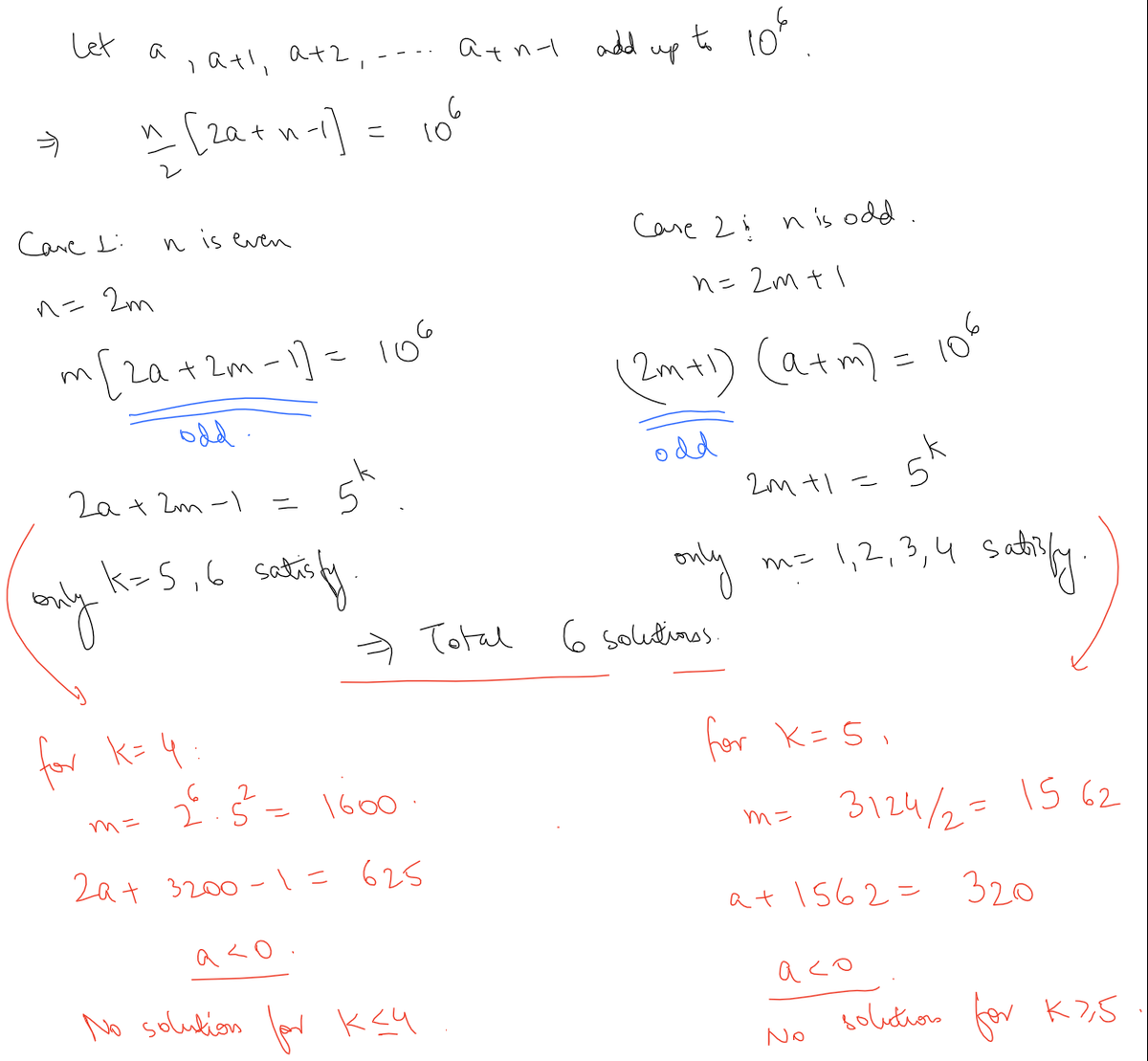
We want to find $0 \le m < n$ such that $10^6$ is the sum of the integers from $m+1$ to $n$ , so that $10^6 \,=\, \tfrac12n(n+1) - \tfrac12m(m+1)$ , and hence $(n-m)(n+m+1) \; = \; 2000000 \; = \; 2^7 \times 5^6$ Thus $n-m$ and $n+m+1$ are positive numbers of opposite parity which multiply to $2000000$ , and $n+m+1 > n-m$ . Thus there are $7$ options: $\begin{array}{|c|c|c|c|} \hline n+m+1 & n-m & n & m \\ \hline 2^7\times5^6 & 1 & 1000000 & 999999 \\ 2^7 \times5^5 & 5 & 200002 & 199997 \\ 2^7 \times5^4 & 5^2 & 40012 & 39987 \\ 2^7 \times5^3 & 5^3 & 8062 & 7937 \\ 2^7 \times5^2 & 5^4 & 1912 & 1287 \\ 5^5 & 2^7 \times 5 & 1882 & 1242 \\ 5^6 & 2^7 & 7876 & 7748 \\ \hline \end{array}$ The first option is not valid, since it just writes $1000000$ as the sum of the single integer $1000000$ . The other $6$ are valid solutions, writing $1000000$ as the sum of $n-m = 5,25,125,625,640,128$ consecutive integers respectively. These solutions include the two given in the question, so there are $\boxed{4}$ other solutions.