Distinct Incircles
 How many distinct right triangles with integer sides circumscribe a circle of radius 10?
How many distinct right triangles with integer sides circumscribe a circle of radius 10?
Note: by distinct I mean we do not count any permutation of ( a , b ) .
e.g. The Pythagorean triple (12, 5 ,13) describes the same triangle as (5, 12 ,13) .
This problem was inspired by the Jiu Zhang Suan Shu
The answer is 6.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Nice solution. I took a slightly different approach ....
Letting the triangle Δ A B C as oriented in the diagram be right-angled at B and with upper vertex A , label the points of tangency of the inscribed circle with sides A B , B C , A C be P , Q , R , respectively.
We then require that ∣ B P ∣ = ∣ B Q ∣ = 1 0 . Letting ∣ A P ∣ = ∣ A R ∣ = x and ∣ C R ∣ = ∣ C Q ∣ = y and applying Pythagoras to Δ A B C we see that
( x + 1 0 ) 2 + ( y + 1 0 ) 2 = ( x + y ) 2 ⟹ 2 0 x + 2 0 y + 1 0 0 = 2 x y
⟹ x y − 1 0 x − 1 0 y = 1 0 0 ⟹ ( x − 1 0 ) ( y − 1 0 ) = 2 0 0 .
Now 2 0 0 = 2 3 5 2 has ( 3 + 1 ) ( 2 + 1 ) = 1 2 positive divisors, and thus (as 2 0 0 is not a perfect square) has 6 distinct divisor "pairs" ( a , b ) such that a b = 2 0 0 with a > b . Then with a = x − 1 0 and b = y − 1 0 each of these 6 divisor pairs corresponds to a unique pair ( x , y ) , which in turn corresponds to a unique Pythagorean triple with inradius 1 0 .
Thus the desired answer is 6 .
Edit: I just noticed that this is the same as Boon Yang's approach. I'll leave this as a comment anyway since it may be easier for some to read.
You should've also included why you chose to check only those values of b that are in [ 2 1 ; 3 4 ] .
Log in to reply
Ah, sorry, when you check for values for b > 3 4 , you will notice that a < b , which tell us that we will obtain the same values but permuted. Also, if you check for 1 0 ≤ b < 2 1 , you don't obtain positive values. Finally, if you check for b < 1 0 , you don't obtain integer values and the initial condition doesn't get satisfied.
Good use of number theory for this geometry-ish problem.
10 [a + b + sqrt(a^2 + b^2 )] = a b
=> b = (200 - 20 a)/(20 - a)
Found (a, b) of (21, 220), (22, 120), (24, 70), (25, 60), (28, 45), (30, 40) and (40, 30), (45, 28), (60, 25), (70, 24), (120, 22), (220, 21) by using Excel with 200 rows. Distinct total is therefore 6.
Hey what i did was this Let b be the hypotenuse.now → s-b=10 → a+c-b=20 《1》
Squring 《1》and using the information that a²+c²=b² We get b²+ac-bc-ab=200 → (b-c)(b-a)= 200 《2》
Using 《2》and the fact that a,b,c are integers and a+c-b=20.
I am getting only five solutions excluding (220, 21).
I am not able to find the mistake in my solution. Can you please help me.
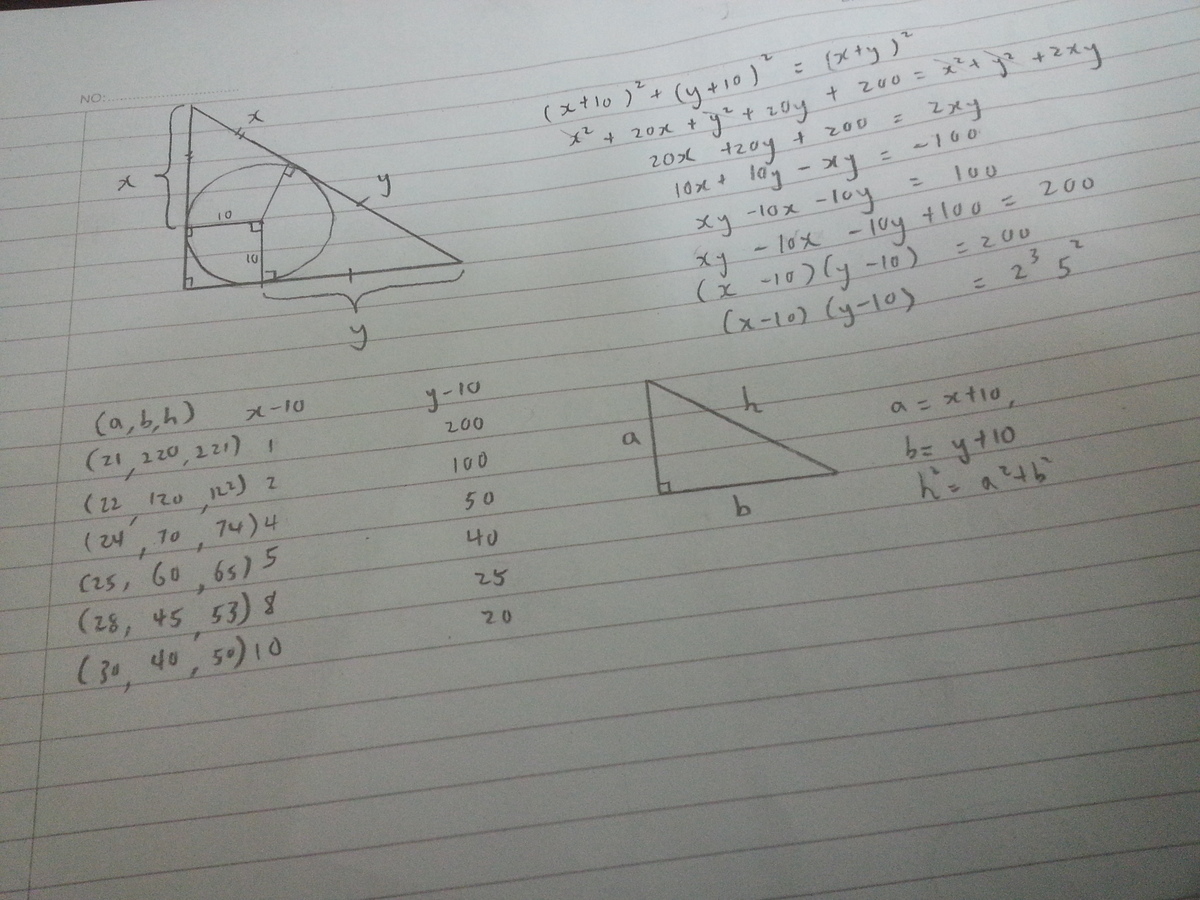
The formula for the inradius of a right triangle with legs a , b and hypothenuse c is: r = 2 a + b − c . Now, we need that:
1 0 = 2 a + b − c ⇒ 2 0 = a + b − c
Since it's a right triangle, we can write:
2 0 = a + b − a 2 + b 2
Rearrange and solve for any of the variables, let's choose a :
( a + b ) − 2 0 = ( a + b ) 2 − 2 a b
( a + b ) 2 − 4 0 ( a + b ) + 4 0 0 = ( a + b ) 2 − 2 a b
4 0 0 = 4 0 ( a + b ) − 2 a b
2 0 0 = 2 0 a + 2 0 b − a b
a ( 2 0 − b ) = 2 0 0 − 2 0 b
a = 2 0 − b 2 0 0 − 2 0 b
We will impose the condition a > b , so we will only check for 2 1 ≤ b ≤ 3 4 . And the only integer distinct solutions for ( a , b ) are: ( 2 2 0 , 2 1 ) , ( 1 2 0 , 2 2 ) , ( 7 0 , 2 4 ) , ( 6 0 , 2 5 ) , ( 4 5 , 2 8 ) and ( 4 0 , 3 0 ) . Hence, there are 6 distinct right triangles.